Профиль компактности

Материал из MachineLearning.

(Различия между версиями)
Перейти к: навигация, поиск
(Новая: {{TOCright}} '''Профиль компактности''' выборки в метрических алгоритмах [[клас...)
Текущая версия (17:30, 21 февраля 2010) (править) (отменить)
(ссылки)
 
(7 промежуточных версий не показаны.)
Строка 7: Строка 7:
Имеется множество объектов <tex>X</tex> и множество имён классов <tex>Y</tex>.
Имеется множество объектов <tex>X</tex> и множество имён классов <tex>Y</tex>.
Задана [[обучающая выборка]] пар «объект—ответ»
Задана [[обучающая выборка]] пар «объект—ответ»
-
<tex>X^m = \{(x_1,y_1),\dots,(x_m,y_m)\} \in X\times Y</tex>.
+
<tex>X^m = \{(x_1,y_1),\ldots,(x_m,y_m)\} \in X\times Y</tex>.
Пусть на множестве объектов задана функция расстояния <tex>\rho(x,x')</tex>.
Пусть на множестве объектов задана функция расстояния <tex>\rho(x,x')</tex>.
Эта функция должна быть достаточно адекватной ''моделью сходства'' объектов.
Эта функция должна быть достаточно адекватной ''моделью сходства'' объектов.
-
Чем больше значение этой функции, тем менее схожими являются два объекта <tex>x,x'</tex>.
+
Чем меньше значение этой функции, тем более схожи объекты <tex>x,x'</tex>.
Для произвольного объекта <tex>u</tex> расположим
Для произвольного объекта <tex>u</tex> расположим
объекты обучающей выборки <tex>x_i</tex> в порядке возрастания расстояний до <tex>u</tex>:
объекты обучающей выборки <tex>x_i</tex> в порядке возрастания расстояний до <tex>u</tex>:
::<tex>\rho(u,x_{1; u}) \leq \rho(u,x_{2; u}) \leq \cdots \leq \rho(u,x_{m; u}),</tex>
::<tex>\rho(u,x_{1; u}) \leq \rho(u,x_{2; u}) \leq \cdots \leq \rho(u,x_{m; u}),</tex>
-
где через <tex>x_{i; u}</tex> обозначается <tex>i</tex>-й сосед объекта <tex>u</tex>.
+
где через <tex>x_{i; u}</tex> обозначается элемент обучающей выборки, который является <tex>i</tex>-м соседом объекта&nbsp;<tex>u</tex>.
Аналогичное обозначение введём и для ответа на <tex>i</tex>-м соседе:
Аналогичное обозначение введём и для ответа на <tex>i</tex>-м соседе:
<tex>y_{i; u}</tex>.
<tex>y_{i; u}</tex>.
Каждый объект <tex>u\in X</tex> порождает свою перенумерацию выборки.
Каждый объект <tex>u\in X</tex> порождает свою перенумерацию выборки.
-
Рассматривается [[метод ближайшего соседа]], который относит классифицируемый объект <tex>u</tex> к тому классу <tex>y_i</tex>, которому принадлежит ближайший объект обучающей выборки <tex>x_i</tex>:
+
Рассматривается [[метод ближайшего соседа]], который относит классифицируемый объект <tex>u</tex> к тому классу, которому принадлежит ближайший к <tex>u</tex> объект обучающей выборки:
-
::<tex>a(u) = y_{1;u}.</tex>
+
::<tex>a(u,X^m) = y_{1;u}.</tex>
 +
 
 +
[[Изображение:ChartLib-1NNProfile.png‎|frame]]
'''Определение.'''
'''Определение.'''
''Профиль компактности'' выборки <tex>X^m</tex> есть функция
''Профиль компактности'' выборки <tex>X^m</tex> есть функция
-
::<tex>R(j,X^m) = \frac1m \sum_{i=1}^L \left[ y_i \neq y_{j;x_i} \right].</tex>
+
::<tex>R(j,X^m) = \frac1m \sum_{i=1}^m \left[ y_i \neq y_{j;x_i} \right].</tex>
 +
 
 +
Иными словами, ''профиль компактности'' <tex>R(j)</tex> —&nbsp;это доля объектов выборки, для которых <tex>j</tex>-й сосед лежит в другом классе.
Профиль компактности является формальным выражением
Профиль компактности является формальным выражением
Строка 36: Строка 40:
В&nbsp;сложных задачах или при неудачном выборе функции расстояния
В&nbsp;сложных задачах или при неудачном выборе функции расстояния
ближайшие объекты практически не&nbsp;несут информации о&nbsp;классах,
ближайшие объекты практически не&nbsp;несут информации о&nbsp;классах,
-
и&nbsp;профиль вырождается в&nbsp;константу, близкую к&nbsp;$0{.}5$, см.&nbsp;Рис.
+
и&nbsp;профиль вырождается в&nbsp;константу, близкую к&nbsp;0.5.
 +
 
 +
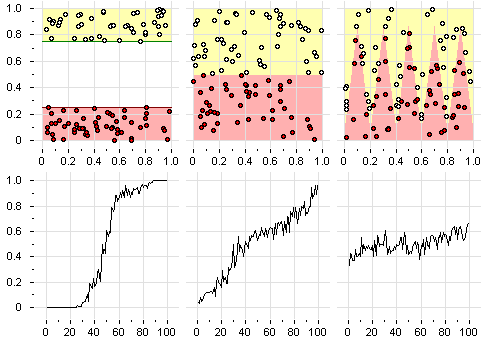
На рисунке показаны профили компактности для серии плоских модельных задач классификации с двумя классами.
 +
Чем ниже проходит начальный участок профиля,
 +
тем выше [[обобщающая способность]] метода ближайшего соседа.
== Связь с полным скользящем контролем ==
== Связь с полным скользящем контролем ==
 +
 +
Выборка <tex>X^L</tex> разбивается всевозможными <tex>N=C_L^k</tex> способами на две непересекающиеся подвыборки:
 +
<tex>X^L = X^m_n \cup X^k_n</tex>,
 +
где
 +
<tex>X^m_n</tex> — обучающая подвыборка длины&nbsp;<tex>m</tex>,
 +
<tex>X^k_n</tex> — контрольная подвыборка длины <tex>k=L-m</tex>,
 +
<tex>n=1,\ldots,N</tex> — номер разбиения.
 +
 +
Для каждого разбиения <tex>n</tex> строится алгоритм <tex>a_n(u,X^m_n)</tex>.
 +
Функционал ''полного скользящего контроля'' (complete cross-validation, CCV)
 +
определяется как средняя (по всем разбиениям) ошибка на контроле:
 +
::<tex>CCV(X^L)=\frac1N \sum_{n=1}^N \frac1k \sum_{x_i \in X^k_n} \left[ a_n(x_i,X^m_n) \neq y_i \right].</tex>
 +
 +
Функционал ''полного скользящего контроля'' характеризует [[обобщающая способность|обобщающую способность]] метода ближайшего соседа
 +
'''Теорема.'''
'''Теорема.'''
 +
Справедлива формула для эффективного вычисления CCV через профиль компактности:
 +
::<tex>CCV(X^L)= \sum_{j=1}^k R(j,X^L) \Gamma(j),</tex>
 +
где <tex>\Gamma(j) = \frac{C_{L-1-j}^{m-1}}{C_{L-1}^{m}}.</tex>
 +
 +
Комбинаторный множитель <tex>\Gamma(j)</tex> быстро убывает с ростом&nbsp;<tex>j</tex>.
 +
Поэтому для минимизации функционала CCV достаточно, чтобы при малых <tex>j</tex> профиль <tex>R(j,X^L)</tex> принимал значения, близкие к нулю.
 +
Но&nbsp;это и&nbsp;означает, что близкие объекты должны лежать преимущественно в&nbsp;одном классе.
 +
Таким образом, профиль действительно является формальным выражением [[гипотеза компактности|гипотезы компактности]].
 +
 +
== Отбор опорных объектов (столпов) путём минимизации CCV ==
 +
В статье [Воронцов, Колосков] процедура оптимизации профиля компактности положена в основу нового алгоритма выделения опорных объектов. В отличие от алгоритма СТОЛП, основанного на «жадной» стратегии последовательного добавления опорных объектов [Загоруйко, 2008], данный алгоритм работает в противоположном направлении — начиная с полной выборки, он последовательно исключает объекты. На каждом шаге выбирается тот объект, исключение которого минимизирует CCV. Оказывается, что процесс отсева объектов разбивается на две стадии. Сначала исключаются ''шумовые выбросы'', что приводит к понижению начального (левого) участка профиля и уменьшению CCV. Затем исключаются неинформативные ''периферийные объекты''. При этом изменяется правый участок профиля, а значение функционала практически не изменяется. Процесс останавливается, когда остаются объекты, исключение которых заметно увеличивает CCV, это и есть ''столпы'' или ''опорные объекты''.
 +
Таким образом, возникает естественное деление обучающих объектов на шумовые, периферийные и опорные.
 +
Эксперименты показывают, что при отборе объектов по критерию CCV практически нет переобучения.
 +
В&nbsp;процессе отсева шумовых и периферийных объектов число ошибок на независимой тестовой выборке изменяется практически синхронно со значением CCV, вычисляемым по обучающей выборке.
== См. также ==
== См. также ==
Строка 47: Строка 84:
* [[Гипотеза компактности]]
* [[Гипотеза компактности]]
* [[Полный скользящий контроль]]
* [[Полный скользящий контроль]]
 +
* [[Функция конкурентного сходства]]
 +
* [[Алгоритм СТОЛП]]
 +
* [[Алгоритм FRiS-СТОЛП]]
== Литература ==
== Литература ==
-
# ''Воронцов К. В.'' [www.ccas.ru/frc/papers/voron04mpc.pdf Комбинаторный подход к оценке качества обучаемых алгоритмов] // Математические вопросы кибернетики / Под ред. О. Б. Лупанов. — М.: Физматлит, 2004. — Т. 13. — С. 5–36.
+
# ''Mullin M.'', ''Sukthankar R.'' [http://citeseer.ist.psu.edu/309025.html Complete cross-validation for nearest neighbor classifiers] // Proceedings of International Conference on Machine Learning. — 2000.
-
# ''Воронцов К. В.'', ''Колосков А. О.'' [www.ccas.ru/frc/papers/students/VoronKoloskov05mmro.pdf Профили компактности и выделение опорных объектов в метрических алгоритмах классификации] // Искусственный Интеллект. — 2006. — С. 30–33.
+
# ''[[Участник:Vokov|Воронцов К. В.]]'' [http://www.ccas.ru/frc/papers/voron04mpc.pdf Комбинаторный подход к оценке качества обучаемых алгоритмов] // Математические вопросы кибернетики / Под ред. О. Б. Лупанов. — М.: Физматлит, 2004. — Т. 13. — С. 5–36.
 +
# ''[[Участник:Vokov|Воронцов К. В.]]'', ''Колосков А. О.'' [http://www.ccas.ru/frc/papers/students/VoronKoloskov05mmro.pdf Профили компактности и выделение опорных объектов в метрических алгоритмах классификации] // Искусственный Интеллект. — 2006. — С. 30–33.
 +
# ''[[Загоруйко, Николай Григорьевич|Zagoruiko N. G.]]'', ''Borisova I. A.'', ''Dyubanov V. V.'', ''Kutnenko O. A.'' Methods of Recognition Based on the Function of Rival Similarity // Pattern Recognition and Image Analisys. 2008. Vol 18. №1. P. 1-6.
 +
# ''[[Загоруйко, Николай Григорьевич|Загоруйко Н. Г.]]'' Интеллектуальный анализ данных, основанный на функции конкурентного сходства // Автометрия, 2008. Том 44, №3. — C. 31-40.
 +
# ''Борисова И.А.'', ''Дюбанов В.В.'', ''[[Загоруйко, Николай Григорьевич|Загоруйко Н. Г.]]'', ''Кутненко О.А.'' [[Media:Borisova2009mmro14.pdf|Сходство и компактность]] // Труды ММРО-14, Суздаль, 2009. — С.89–-92.
[[Категория:Метрические алгоритмы классификации]]
[[Категория:Метрические алгоритмы классификации]]
[[Категория:Теория вычислительного обучения]]
[[Категория:Теория вычислительного обучения]]

Текущая версия

Содержание

Профиль компактности выборки в метрических алгоритмах классификации — функция R(j), выражающая долю объектов выборки, для которых правильный ответ не совпадает с правильным ответом на j-м соседе.

Определения

Рассматривается задача классификации. Имеется множество объектов X и множество имён классов Y. Задана обучающая выборка пар «объект—ответ» X^m = \{(x_1,y_1),\ldots,(x_m,y_m)\} \in X\times Y.

Пусть на множестве объектов задана функция расстояния \rho(x,x'). Эта функция должна быть достаточно адекватной моделью сходства объектов. Чем меньше значение этой функции, тем более схожи объекты x,x'.

Для произвольного объекта u расположим объекты обучающей выборки x_i в порядке возрастания расстояний до u:

\rho(u,x_{1; u}) \leq \rho(u,x_{2; u}) \leq \cdots \leq \rho(u,x_{m; u}),

где через x_{i; u} обозначается элемент обучающей выборки, который является i-м соседом объекта u. Аналогичное обозначение введём и для ответа на i-м соседе: y_{i; u}. Каждый объект u\in X порождает свою перенумерацию выборки.

Рассматривается метод ближайшего соседа, который относит классифицируемый объект u к тому классу, которому принадлежит ближайший к u объект обучающей выборки:

a(u,X^m) = y_{1;u}.

Определение. Профиль компактности выборки X^m есть функция

R(j,X^m) = \frac1m \sum_{i=1}^m \left[ y_i \neq y_{j;x_i} \right].

Иными словами, профиль компактности R(j) — это доля объектов выборки, для которых j-й сосед лежит в другом классе.

Профиль компактности является формальным выражением гипотезы компактности — предположения о том, что схожие объекты гораздо чаще лежат в одном классе, чем в разных. Чем проще задача, то есть чем чаще близкие объекты оказываются в одном классе, тем сильнее «прижимается к нулю» начальный участок профиля. В сложных задачах или при неудачном выборе функции расстояния ближайшие объекты практически не несут информации о классах, и профиль вырождается в константу, близкую к 0.5.

На рисунке показаны профили компактности для серии плоских модельных задач классификации с двумя классами. Чем ниже проходит начальный участок профиля, тем выше обобщающая способность метода ближайшего соседа.

Связь с полным скользящем контролем

Выборка X^L разбивается всевозможными N=C_L^k способами на две непересекающиеся подвыборки: X^L = X^m_n \cup X^k_n, где X^m_n — обучающая подвыборка длины m, X^k_n — контрольная подвыборка длины k=L-m, n=1,\ldots,N — номер разбиения.

Для каждого разбиения n строится алгоритм a_n(u,X^m_n). Функционал полного скользящего контроля (complete cross-validation, CCV) определяется как средняя (по всем разбиениям) ошибка на контроле:

CCV(X^L)=\frac1N \sum_{n=1}^N \frac1k \sum_{x_i \in X^k_n} \left[ a_n(x_i,X^m_n) \neq y_i \right].

Функционал полного скользящего контроля характеризует обобщающую способность метода ближайшего соседа

Теорема. Справедлива формула для эффективного вычисления CCV через профиль компактности:

CCV(X^L)= \sum_{j=1}^k R(j,X^L) \Gamma(j),

где \Gamma(j) = \frac{C_{L-1-j}^{m-1}}{C_{L-1}^{m}}.

Комбинаторный множитель \Gamma(j) быстро убывает с ростом j. Поэтому для минимизации функционала CCV достаточно, чтобы при малых j профиль R(j,X^L) принимал значения, близкие к нулю. Но это и означает, что близкие объекты должны лежать преимущественно в одном классе. Таким образом, профиль действительно является формальным выражением гипотезы компактности.

Отбор опорных объектов (столпов) путём минимизации CCV

В статье [Воронцов, Колосков] процедура оптимизации профиля компактности положена в основу нового алгоритма выделения опорных объектов. В отличие от алгоритма СТОЛП, основанного на «жадной» стратегии последовательного добавления опорных объектов [Загоруйко, 2008], данный алгоритм работает в противоположном направлении — начиная с полной выборки, он последовательно исключает объекты. На каждом шаге выбирается тот объект, исключение которого минимизирует CCV. Оказывается, что процесс отсева объектов разбивается на две стадии. Сначала исключаются шумовые выбросы, что приводит к понижению начального (левого) участка профиля и уменьшению CCV. Затем исключаются неинформативные периферийные объекты. При этом изменяется правый участок профиля, а значение функционала практически не изменяется. Процесс останавливается, когда остаются объекты, исключение которых заметно увеличивает CCV, это и есть столпы или опорные объекты. Таким образом, возникает естественное деление обучающих объектов на шумовые, периферийные и опорные. Эксперименты показывают, что при отборе объектов по критерию CCV практически нет переобучения. В процессе отсева шумовых и периферийных объектов число ошибок на независимой тестовой выборке изменяется практически синхронно со значением CCV, вычисляемым по обучающей выборке.

См. также

Литература

  1. Mullin M., Sukthankar R. Complete cross-validation for nearest neighbor classifiers // Proceedings of International Conference on Machine Learning. — 2000.
  2. Воронцов К. В. Комбинаторный подход к оценке качества обучаемых алгоритмов // Математические вопросы кибернетики / Под ред. О. Б. Лупанов. — М.: Физматлит, 2004. — Т. 13. — С. 5–36.
  3. Воронцов К. В., Колосков А. О. Профили компактности и выделение опорных объектов в метрических алгоритмах классификации // Искусственный Интеллект. — 2006. — С. 30–33.
  4. Zagoruiko N. G., Borisova I. A., Dyubanov V. V., Kutnenko O. A. Methods of Recognition Based on the Function of Rival Similarity // Pattern Recognition and Image Analisys. 2008. Vol 18. №1. P. 1-6.
  5. Загоруйко Н. Г. Интеллектуальный анализ данных, основанный на функции конкурентного сходства // Автометрия, 2008. Том 44, №3. — C. 31-40.
  6. Борисова И.А., Дюбанов В.В., Загоруйко Н. Г., Кутненко О.А. Сходство и компактность // Труды ММРО-14, Суздаль, 2009. — С.89–-92.
Источник — «http://machinelearning.ru/wiki/index.php?title=%D0%9F%D1%80%D0%BE%D1%84%D0%B8%D0%BB%D1%8C_%D0%BA%D0%BE%D0%BC%D0%BF%D0%B0%D0%BA%D1%82%D0%BD%D0%BE%D1%81%D1%82%D0%B8»
Личные инструменты