Нормальное распределение

Материал из MachineLearning.

(Различия между версиями)

Текущая версия

**Нормальное распределение**
Плотность вероятности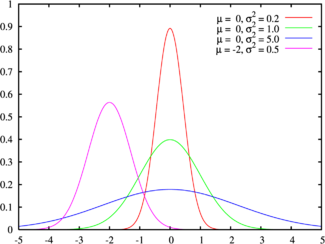 Зеленая линия соответствует стандартному нормальному распределению
Функция распределения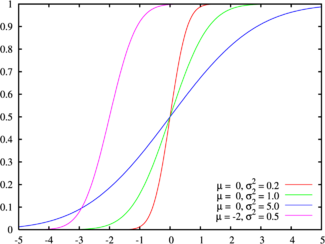 Цвета на этом графике соответствуют графику наверху
Параметры	$\mu$ - коэффициент сдвига (вещественное число) $\sigma>0$ - коэффициент масштаба (вещественный, строго положительный)
Носитель	$x \in (-\infty;+\infty)\!$
Плотность вероятности	$\frac1{\sigma\sqrt{2\pi}}\; \exp\left(-\frac{\left(x-\mu\right)^2}{2\sigma^2} \right) \!$
Функция распределения	$\frac1{\sigma\sqrt{2\pi}}\;\int\limits_{-\infty}^{x} \exp\left(-\frac{\left(t-\mu\right)^2}{2\sigma^2} \right) dt\!$
Математическое ожидание	$\mu\,$
Медиана	$\mu\,$
Мода	$\mu\,$
Дисперсия	$\sigma^2\,$
Коэффициент асимметрии	$0\,$
Коэффициент эксцесса	$0\,$
Информационная энтропия	$\ln\left(\sigma\sqrt{2\,\pi\,e}\right)\!$
Производящая функция моментов	$M_X(t)= \exp\left(\mu\,t+\frac{\sigma^2 t^2}{2}\right)$
Характеристическая функция	$\phi_X(t)=\exp\left(\mu\,i\,t-\frac{\sigma^2 t^2}{2}\right)$

Нормальное распределение, также называемое распределением Гаусса, — распределение вероятностей, которое играет важнейшую роль во многих областях знаний, особенно в физике. Физическая величина подчиняется нормальному распределению, когда она подвержена влиянию огромного числа случайных помех. Ясно, что такая ситуация крайне распространена, поэтому можно сказать, что из всех распределений в природе чаще всего встречается именно нормальное распределение — отсюда и произошло одно из его названий.

Нормальное распределение зависит от двух параметров — смещения и масштаба, то есть является с математической точки зрения не одним распределением, а целым их семейством. Значения параметров соответствуют значениям среднего (математического ожидания) и разброса (стандартного отклонения).

Стандартным нормальным распределением называется нормальное распределение с математическим ожиданием 0 и стандартным отклонением 1.

Содержание

1 Моделирование нормальных случайных величин
2 Свойства
3 Статистическая проверка принадлежности нормальному распределению
4 Многомерное нормальное распределение
5 Замечания
6 Свойства многомерного нормального распределения
7 См. также
8 Заключение

Моделирование нормальных случайных величин

Простейшие, но неточные методы моделирования основываются на центральной предельной теореме. Именно, если сложить много независимых одинаково распределённых величин с конечной дисперсией, то сумма будет распределена примерно нормально. Например, если сложить 12 независимых базовых случайных величин, получится грубое приближение стандартного нормального распределения. Тем не менее, с увеличением слагаемых распределение суммы стремится к нормальному.

Использование точных методов предпочтительно, поскольку у них практически нет недостатков. В частности, преобразование Бокса — Мюллера является точным, быстрым и простым для реализации методом генерации.

Свойства

Если случайные величины $X_1$ и $X_2$ независимы и имеют нормальное распределение с математическими ожиданиями $\mu_1$ и $\mu_2$ и дисперсиями $\sigma_1^2$ и $\sigma_2^2$ соответственно, то $X_1+X_2$ также имеет нормальное распределение с математическим ожиданием $\mu_1+\mu_2$ и дисперсией $\sigma_1^2+\sigma_2^2$ .

Статистическая проверка принадлежности нормальному распределению

Поскольку нормальное распределение часто встречается на практике, то для него разработаны специальные статистические критерии проверки на «нормальность»:

Критерий согласия Пирсона
Критерий Колмогорова-Смирнова
Критерий Андерсона-Дарлинга
Критерий Жака-Бера
Критерий Шапиро-Вилка
График нормальности — не столько критерий, сколько графическая иллюстрация: точки специально построенного графика должны лежать почти на одной прямой.

Многомерное нормальное распределение

Многоме́рное норма́льное распределе́ние (или многоме́рное га́уссовское распределе́ние) в теории вероятностей — это обобщение одномерного нормального распределения.

Случайный вектор $\mathbf{X} = (X_1,\ldots, X_n)^{\top}: \Omega \to \mathbb{R}^n$ имеет многомерное нормальное распределение, если выполняется одно из следующих эквивалентных условий:

Произвольная линейная комбинация компонентов вектора $\sum\limits_{i=1}^n a_i X_i$ имеет нормальное распределение или является константой.
Существует вектор независимых стандартных нормальных случайных величин $\mathbf{Z}=(Z_1,\ldots, Z_m)^{\top}$ , вещественный вектор $\mathbf{\mu} = (\mu_1,\ldots, \mu_m)^{\top}$ и матрица $\mathbf{A}$ размерности $n \times m$ , такие что:

$\mathbf{X} = \mathbf{A} \mathbf{Z} + \mathbf{\mu}$ .

Существует вектор $\mathbf{\mu} \in \mathbb{R}^n$ и неотрицательно определённая симметричная матрица $\mathbf{\Sigma}$ размерности $n \times n$ , такие что плотность вероятности вектора $\mathbf{X}$ имеет вид:

$f_{\mathbf{X}}(\mathbf{x}) = \frac{1}{(2\pi )^{n/2} | \Sigma |^{1/2}} e^{-\frac{1}{2}(\mathbf{x} - \mathbf{\mu})^{\top} \Sigma^{-1} (\mathbf{x} - \mathbf{\mu})},\; \mathbf{x} \in \mathbb{R}^n$ ,

где $| \Sigma |$ — определитель матрицы $\Sigma$ , а $\Sigma^{-1}$ — матрица обратная к $\Sigma$ .

Существует вектор $\mathbf{\mu} \in \mathbb{R}^n$ и неотрицательно определённая симметричная матрица $\mathbf{\Sigma}$ размерности $n \times n$ , такие что характеристическая функция вектора $\mathbf{X}$ имеет вид:

$\phi_{\mathbf{X}}(\mathbf{u}) = e^{i \mathbf{\mu}^{\top} \mathbf{u} - \frac{1}{2}\mathbf{u}^{\top} \Sigma \mathbf{u}},\; \mathbf{u} \in \mathbb{R}^n$ .

Замечания

Если одно из приведённых выше определений принято в качестве основного, то другие выводятся в качестве теорем.
Вектор $\mathbf{\mu}$ является вектором средних значений $\mathbf{X}$ , а $\Sigma$ — его ковариационная матрица.
В случае $n = 1$ , многомерное нормальное распределение сводится к обычному нормальному распределению.
Если случайный вектор $\mathbf{X}$ имеет многомерное нормальное распределение, то пишут $\mathbf{X} \sim \mathrm{N}(\mathbf{\mu},\Sigma)$ .

Свойства многомерного нормального распределения

Если вектор $\mathbf{X} = (X_1,\ldots, X_n)^{\top}$ имеет многомерное нормальное распределение, то его компоненты $X_i, i=1,\ldots, n,$ имеют одномерное нормальное распределение. Обратное, вообще говоря, неверно!
Если случайные величины $X_1,\ldots,X_n$ имеют одномерное нормальное распределение и совместно независимы, то случайный вектор $\mathbf{X} = (X_1,\ldots, X_n)^{\top}$ имеет многомерное нормальное распределение. Матрица ковариаций $\Sigma$ такого вектора диагональна.
Если $\mathbf{X} = (X_1,\ldots, X_n)^{\top}$ имеет многомерное нормальное распределение, и его компоненты попарно некоррелированы, то они независимы. Однако, если только компоненты $X_i,\; i = 1 , \ldots, n$ имеют одномерное нормальное распределение и попарно не коррелируют, то отсюда не следует, что они независимы.

Контрпример. Пусть $X \sim \mathrm{N}(0,1)$ , а $\alpha = \pm 1$ с равными вероятностями. Тогда если $Y = \alpha X \sim \mathrm{N}(0,1)$ , то корреляция $X$ и $Y$ равна нулю. Однако, эти случайные величины зависимы.

Многомерное нормальное распределение устойчиво относительно линейных преобразований. Если $\mathbf{X} \sim \mathrm{N}(\mathbf{\mu},\Sigma)$ , а $\mathbf{A}$ — произвольная матрица размерности $m \times n$ , то

$\mathbf{A}\mathbf{X} \sim \mathrm{N}\left(\mathbf{A}\mathbf{\mu},\mathbf{A}\Sigma \mathbf{A}^{\top}\right)$ .

См. также

Таблица значений функции распределения стандартной нормальной случайной величины

Заключение

Нормальное распределение наиболее часто встречается в природе, нормально распределёнными являются следующие случайные величины:

отклонение при стрельбе
ошибки при измерениях
рост человека

Такое широкое распространение закона связано с тем, что он является предельным законом, к которому приближаются многие другие (например, биномиальный). Доказано, что сумма очень большого числа случайных величин, влияние каждой из которых близко к 0, имеет распределение, близкое к нормальному. Этот факт является содержанием предельной теоремы Ляпунова.

Источник — «http://machinelearning.ru/wiki/index.php?title=%D0%9D%D0%BE%D1%80%D0%BC%D0%B0%D0%BB%D1%8C%D0%BD%D0%BE%D0%B5_%D1%80%D0%B0%D1%81%D0%BF%D1%80%D0%B5%D0%B4%D0%B5%D0%BB%D0%B5%D0%BD%D0%B8%D0%B5»

Категория: Вероятностные распределения

@@ Строка 2: / Строка 2: @@
   name       =Нормальное распределение|
   type       =Плотность|
-  pdf_image  =[[Файл:Normal distribution pdf.png|325px|Плотность нормального распределения]]<br /><small>Зеленая линия соответствует стандартному нормальному распределению</small>|
+  pdf_image  =[[Изображение:Normal_distribution_pdf.png|325px|Плотность нормального распределения]]<br /><small>Зеленая линия соответствует стандартному нормальному распределению</small>|
-  cdf_image  =[[Файл:Normal distribution cdf.png|325px|Функция распределения нормального распределения]]<br /><small>Цвета на этом графике соответствуют графику наверху</small>|
+  cdf_image  =[[Изображение:Normal_distribution_cdf.png|325px|Функция распределения нормального распределения]]<br /><small>Цвета на этом графике соответствуют графику наверху</small>|
   parameters =<tex>\mu</tex> - [[коэффициент сдвига]] ([[вещественное число]])<br/><tex>\sigma>0</tex> - [[коэффициент масштаба]] (вещественный, строго положительный)|
   support    =<tex>x \in (-\infty;+\infty)\!</tex>|
   pdf        =<tex>\frac1{\sigma\sqrt{2\pi}}\; \exp\left(-\frac{\left(x-\mu\right)^2}{2\sigma^2} \right) \!</tex>|
-  cdf        =<tex>\frac1{\sigma\sqrt{2\pi}}\;\int\limits_{-\infin}^{x} \exp\left(-\frac{\left(t-\mu\right)^2}{2\sigma^2} \right) dt\!</tex>|
+  cdf        =<tex>\frac1{\sigma\sqrt{2\pi}}\;\int\limits_{-\infty}^{x} \exp\left(-\frac{\left(t-\mu\right)^2}{2\sigma^2} \right) dt\!</tex>|
   mean       =<tex>\mu\,</tex>|
   median     =<tex>\mu\,</tex>|
@@ Строка 36: / Строка 36: @@
 <!-- not checked -->
 Поскольку нормальное распределение часто встречается на практике, то для него разработаны специальные статистические критерии проверки на «нормальность»:
-* [[Критерий согласия Пирсона|Критерий Пирсона]]
+* [[Критерий хи-квадрат|Критерий согласия Пирсона]]
-* [[Критерий согласия Колмогорова|Критерий Колмогорова-Смирнова]]
+* [[Критерий Колмогорова-Смирнова|Критерий Колмогорова-Смирнова]]
-* {{не переведено|есть=:en:Anderson-Darling test|надо=Критерий Андерсона-Дарлинга}}
+* [[Критерий Андерсона-Дарлинга|Критерий Андерсона-Дарлинга]]
-* {{не переведено|есть=:en:Jarque-Bera test|надо=Критерий Жака-Бера}}
+* [[Критерий Жака-Бера|Критерий Жака-Бера]]
-* {{не переведено|есть=:en:Shapiro-Wilk test|надо=Критерий Шапиро-Вилка}}
+* [[Критерий Шапиро-Вилка|Критерий Шапиро-Вилка]]
-* {{не переведено|есть=:en:Rankit|надо=График нормальности}} — не столько критерий, сколько графическая иллюстрация: точки специально построенного графика должны лежать почти на одной прямой.
+* [[График нормальности|График нормальности]] — не столько критерий, сколько графическая иллюстрация: точки специально построенного графика должны лежать почти на одной прямой.
 == Многомерное нормальное распределение ==
@@ Строка 74: / Строка 74: @@
 * Многомерное нормальное распределение [[Устойчивое распределение|устойчиво]] относительно [[Линейный оператор|линейных преобразований]]. Если <tex>\mathbf{X} \sim \mathrm{N}(\mathbf{\mu},\Sigma)</tex>, а <tex>\mathbf{A}</tex> — произвольная матрица размерности <tex>m \times n</tex>, то
 : <tex>\mathbf{A}\mathbf{X} \sim \mathrm{N}\left(\mathbf{A}\mathbf{\mu},\mathbf{A}\Sigma \mathbf{A}^{\top}\right)</tex>.
+==См. также==
+* [http://sprap.ru/0048-1.png  Таблица значений функции распределения стандартной нормальной случайной величины]
 == Заключение ==
@@ Строка 82: / Строка 85: @@
 Такое широкое распространение закона связано с тем, что он является предельным законом, к которому приближаются многие другие (например, биномиальный).
 Доказано, что сумма очень большого числа случайных величин, влияние каждой из которых близко к 0, имеет распределение, близкое к нормальному. Этот факт является содержанием предельной [[Теорема_Ляпунова|теоремы Ляпунова]].
+[[Категория:Вероятностные распределения]]