Критерий Уилкоксона двухвыборочный
Материал из MachineLearning.
(Новая: '''Критерий Уилкоксона двухвыборочный''' (Wilcoxon) — непараметрический статистический критерий == Прим...) |
(→Описание критерия) |
||
| (7 промежуточных версий не показаны.) | |||
| Строка 1: | Строка 1: | ||
| - | + | {{TOCright}} | |
| - | + | '''Критерий Уилкоксона (Вилкоксона) двухвыборочный''' — [[непараметрический статистический критерий]], используемый для оценки различий между двумя выборками, взятыми из закона распределения, отличного от нормального, либо измеренными с использованием [[Теория измерений|порядковой шкалы]]. Имеется [[Критерий_Уилкоксона_для_связных_выборок|аналог]] критерия Уилкоксона для связанных повторных наблюдений. Критерий является [[Ранговый критерий|ранговым]], поэтому он инвариантен по отношению к любому монотонному преобразованию шкалы измерения. | |
| - | + | == Пример задачи == | |
| - | + | Задача — сравнить две методики подготовки роженицы к родам. Сравнивается эффективность по оценке состояния новорожденного в баллах (шкала является [[Теория измерений|порядковой]]). | |
== Описание критерия == | == Описание критерия == | ||
| - | Заданы две выборки <tex>x^m = (x_1,\ldots,x_m),\; x_i \in \mathbb{R};\;\; y^n = (y_1,\ldots,y_n),\; y_i \in \mathbb{R}</tex>. | + | Заданы две выборки <tex>x^m = (x_1,\ldots,x_m),\; x_i \in \mathbb{R};\;\; y^n = (y_1,\ldots,y_n),\; y_i \in \mathbb{R};\; m \le n,</tex> в противном случае следует поменять выборки местами. |
| - | '''Дополнительные предположения:''' | + | '''Дополнительные предположения:''' обе выборки [[простая выборка|простые]], объединённая выборка [[независимая выборка|независима]]; |
| - | + | ||
| - | + | ||
| - | '''[[Нулевая гипотеза]]''' <tex>H_0:\; </tex> | + | '''[[Нулевая гипотеза]]''' <tex>H_0:\; \mathbb{P} \{ x\ <\ y \} = 1/2. </tex> |
| - | ''' | + | '''Вычисление статистики критерия:''' |
| + | # Построить общий вариационный ряд объединённой выборки <tex>x^{(1)} \leq \cdots \leq x^{(m+n)}</tex> и найти ранги <tex>r(x_i),\; r(y_i)</tex> всех элементов обеих выборок в общем вариационном ряду. | ||
| + | # Рассчитать суммы рангов, соответствующих обеим выборкам: | ||
| + | #:<tex>R_x = \sum_{i=1}^m r(x_i);</tex> | ||
| + | #:<tex>R_y = \sum_{i=1}^n r(y_i);</tex> | ||
| + | # Если размеры выборок совпадают (<tex>m=n</tex>), то значение статистики <tex>W</tex> будет равняется одной из сумм рангов <tex>R_x</tex> или <tex>R_y</tex> (любой). Если же выборки не равны, то <tex>W = R_x</tex>, то есть сумме рангов, соответствующей меньшей выборке. Заметим, что статистика <tex>W</tex> линейно связана со статистикой [[Критерий Уилкоксона-Манна-Уитни|U-критерия Манна-Уитни]]. | ||
| - | + | '''Критерий''' (при [[уровень значимости|уровне значимости]] <tex>\alpha</tex>): | |
| - | == | + | Против альтернативы <tex>H_1:\; \mathbb{P} \{ x\ <\ y \} \neq 1/2</tex>: |
| + | |||
| + | :если <tex>W \notin \left[ W_{\alpha/2},\,W_{1-\alpha/2} \right]</tex> , то нулевая гипотеза отвергается. Здесь <tex>W_{\alpha}</tex> есть <tex>\alpha</tex>-[[квантиль]] табличного распределения Уилкоксона с параметрами <tex>m,\,n</tex>. <ref>Кобзарь А. И. Прикладная математическая статистика. — 457 c.</ref><ref>Лапач С. Н. Статистика в науке и бизнесе. — 150 с.</ref> | ||
| + | |||
| + | '''Асимптотический критерий:''' | ||
| + | |||
| + | [[Изображение:Standard_Normal_Density_-_Double-sided_Critical_Area.png|thumb|Критическая область двухвыборочного критерия Уилкоксона (нормальная аппроксимация).]] | ||
| + | |||
| + | Рассмотрим нормированную и центрированную статистика Уилкоксона: | ||
| + | |||
| + | :<tex>\tilde W = \frac{W - \frac{m(m + n + 1)}{2}}{sqrt{\frac{mn(m + n + 1)}{12}}}</tex>; | ||
| + | |||
| + | <tex>\tilde W</tex> асимптотически имеет стандартное нормальное распределение. Нулевая гипотеза (против альтернативы <tex>H_1</tex>) отвергается, если <tex> |\tilde W|\ >\ \Phi_{1-\alpha/2} </tex>, где <tex>\Phi_{\alpha}</tex> есть <tex>\alpha</tex>-[[квантиль]] стандартного нормального распределения. | ||
| + | |||
| + | Приближение можно использовать, если размер хотя бы одной из выборок превышает 25. Если размеры выборок равны, то данная аппроксимация хорошо работает до <tex>m = n = 8</tex>.<ref>Лапач С. Н. Статистика в науке и бизнесе. — 161 с.</ref> | ||
| + | |||
| + | '''Случай совпадающих наблюдений:''' | ||
| + | |||
| + | При наличии [[Вариационный ряд|связок]] необходимо учесть их с помощью поправки. Выражение в знаменателе необходимо заменить на следующее: | ||
| + | |||
| + | :<tex>\left{ \frac{mn(n+m+1)}{12} \left[ 1 - \frac{\sum^k_{i = 1}t_i(t_i^2-1)}{(n+m)(n+m-1)(n+m+1)} \right] \right}^{1/2}.</tex><ref>Кобзарь А. И. Прикладная математическая статистика. — 454 c.</ref><ref>Лагутин М. Б. Наглядная математическая статистика. — 206 с.</ref> | ||
| + | |||
| + | :Здесь <tex>k</tex> - количество только тех связок, в которые входят ранги как одной, так и другой выборок, <tex>t_1, \ldots, t_k</tex> - их размеры. Совпадения, целиком состоящие из элементов одной и той же выборки, на величину <tex>\tilde W</tex> не влияют. Наблюдения, не совпадающие с другими, рассматриваются как связки размера 1. Для элементов связок вычисляется [[Вариационный ряд|средний ранг]]. | ||
| + | |||
| + | '''Поправка:'''<ref>Лагутин М. Б. Наглядная математическая статистика. — 205-206 с.</ref> | ||
| + | |||
| + | В 1976 году Р. Иман предложил следующую аппроксимацию, обеспечивающую значительное снижение относительной ошибки для критических значений, в том числе на малых выборках. Поправка использует полусумму нормальной и стьюдентовской квантилей. Положим <tex>N = n + m</tex>. Тогда: | ||
| + | |||
| + | :<tex>\tilde W^{*} = \frac12 \tilde W \left[ 1 + \sqrt{\frac{N-2}{N - 1 - (\tilde W)^2}} \right]</tex>. | ||
| + | |||
| + | Гипотеза <tex>H_0</tex> отвергается, если <tex>\tilde W ^{*} \ge (x_{1-\alpha}+y_{1-\alpha})/2</tex>, где <tex>x_{1-\alpha},\; y_{1-\alpha}</tex> обозначают соответственно квантили уровня <tex>1-\alpha</tex> стандартного нормального распределения и [[Распределение Стьюдента|распределения Стьюдента]] с <tex>N-2</tex> степенью свободы. | ||
| + | |||
| + | == Применение критерия == | ||
| + | |||
| + | В биологических и эконометрических приложениях метод часто используется для проверки гипотезы о равенстве средних двух независимых выборок. Вообще говоря, данное использование критерия некорректно. Можно построить примеры, когда <tex>\mathbb{P} \{ x<y \} = 1/2</tex>, и средние выборок не совпадают.<ref>Орлов А. И. Эконометрика. — 79 с.</ref> При этом надо заметить, что данный недостаток не является редкостью, о многих популярных в математической статистике критериях можно сказать, что они не позволяют проверять те гипотезы, с которыми традиционно связаны. При применении подобных критериев к анализу реальных данных необходимо тщательно взвешивать их достоинства и недостатки.<ref>Орлов А. И. Эконометрика. — 83 с.</ref> | ||
| + | |||
| + | Критерий является аналогом критерия [[Критерий Стьюдента|t-критерия Стьюдента для независимых выборок]] в случае закона распределения, отличного от нормального, либо данных, измеренных с использованием порядковой шкалы. Для нормально распределённых совокупностей следует использовать более мощный t-критерий. | ||
| + | |||
| + | == Критерий Уилкоксона и [[Критерий Уилкоксона-Манна-Уитни|U-критерий Манна-Уитни]] == | ||
| + | |||
| + | Статистики критериев Уилкоксона и Уилкоксона-Манна-Уитни линейно связаны, поэтому, по сути, нет смысла говорить о двух различных критериях.<ref>Орлов А. И. Эконометрика. — 75 c.</ref> Оба они проверяют одну и ту же гипотезу и их границы применимости также совпадают. В то же время в литературе можно встретить рекомендации использовать критерий Уилкоксона для проверки равенства средних, когда нет предположений о дисперсиях,<ref>Лапач С. Н. Статистика в науке и бизнесе. — 160 с.</ref>, а в случае равных дисперсий применять [[Критерий_Уилкоксона-Манна-Уитни|U-критерий Манна-Уитни]].<ref>Лапач С. Н. Статистика в науке и бизнесе. — 118 с.</ref> | ||
| + | |||
| + | Проведём эксперимент: будем строить график [[Достигаемый уровень значимости|достигаемого уровня значимости]] как функцию размера выборок и параметров распределения. Будем усреднять p-value по нескольким десяткам экспериментов. | ||
| + | |||
| + | Общие параметры для всех экспериментов: | ||
| + | * Выборки генерируются независимо из нормального распределения с заданными параметрами. | ||
| + | * Размер выборок варьируется от 50 до 500 с шагом 50. | ||
| + | * Значение p-value усредняется по 50 экспериментам. | ||
| + | * Размер выборки откладывается по вертикальной оси, переменный параметр по горизонтальной. | ||
| + | |||
| + | |||
| + | {| class="standard" | ||
| + | !Тип критерия | ||
| + | !Параметры эксперимента | ||
| + | !График | ||
| + | |- | ||
| + | |align="center"|[[Критерий Уилкоксона-Манна-Уитни|U-критерий Манна-Уитни]] | ||
| + | |Среднее первой выборки: 0. | ||
| + | |||
| + | Среднее второй выборки: -3:0.3:3.<ref>Запись вида <tex>\alpha\;:\;\delta\;:\;\beta</tex> на языке [[Matlab]] обозначает выборку, составленную из чисел от <tex>\alpha</tex> до <tex>\beta</tex> c шагом <tex>\delta</tex>.</ref> | ||
| + | |||
| + | Дисперсия первой выборки: 5. | ||
| + | |||
| + | Дисперсия второй выборки: 5. | ||
| + | |||
| + | |[[Изображение:UNorm_50-50-1000_0_-3-0.3-3_5_5_50.png|400px]] | ||
| + | |- | ||
| + | |align="center"|Критерий Уилкоксона | ||
| + | |Среднее первой выборки: 0. | ||
| + | |||
| + | Среднее второй выборки: -3:0.3:3. | ||
| + | |||
| + | Дисперсия первой выборки: 5. | ||
| + | |||
| + | Дисперсия второй выборки: 5. | ||
| + | |||
| + | |[[Изображение:WNorm 50-50-1000 0 -3-0.3-3 5 5 50.png|400px]] | ||
| + | |- | ||
| + | |align="center"|[[Критерий Уилкоксона-Манна-Уитни|U-критерий Манна-Уитни]] | ||
| + | |Среднее первой выборки: 0. | ||
| + | |||
| + | Среднее второй выборки: -30:3:30. | ||
| + | |||
| + | Дисперсия первой выборки: 1. | ||
| + | |||
| + | Дисперсия второй выборки: 50. | ||
| + | |||
| + | |[[Изображение:UNorm 50-50-1000 0 -30-3-30 1 50 50.png|400px]] | ||
| + | |- | ||
| + | |||
| + | |align="center"|Критерий Уилкоксона | ||
| + | |Среднее первой выборки: 0. | ||
| + | |||
| + | Среднее второй выборки: -30:3:30. | ||
| + | |||
| + | Дисперсия первой выборки: 1. | ||
| + | |||
| + | Дисперсия второй выборки: 50. | ||
| + | |||
| + | |[[Изображение:WNorm 50-50-1000 0 -30-3-30 1 50 50.png|400px]] | ||
| + | |} | ||
| + | |||
| + | Легко видеть, что при одинаковых параметрах экспериментов графики p-value критериев Уилкоксона и Уилкоксона-Манна-Уитни практически совпадают, в том числе и в случае, когда дисперсии выборок существенно различаются. | ||
| + | |||
| + | == Примечания == | ||
| + | <references/> | ||
== Литература == | == Литература == | ||
# ''Лагутин М. Б.'' Наглядная математическая статистика. В двух томах. — М.: П-центр, 2003. — 204-209 с. | # ''Лагутин М. Б.'' Наглядная математическая статистика. В двух томах. — М.: П-центр, 2003. — 204-209 с. | ||
| - | + | # ''Лапач С. Н. , Чубенко А. В., Бабич П. Н.'' Статистика в науке и бизнесе. — Киев: Морион, 2002. — 160-164 с. | |
| + | # ''Орлов А. И.'' Эконометрика. — М.: Экзамен, 2003. — §4.5. | ||
| + | # ''Кобзарь А. И.'' Прикладная математическая статистика. — М.: Физматлит, 2006. — 454-456 с. | ||
== Ссылки == | == Ссылки == | ||
| - | * [[Проверка статистических гипотез]] — о методологии проверки статистических гипотез. | + | * [[Критерий Уилкоксона-Манна-Уитни]] — аналогичный критерий. |
| - | * [[ | + | * [[Проверка статистических гипотез]] — о методологии проверки статистических гипотез. |
| + | * [[Критерий Уилкоксона для связных выборок]] — аналог критерия для случая парных повторных наблюдений. | ||
| - | |||
[[Категория:Непараметрические статистические тесты]] | [[Категория:Непараметрические статистические тесты]] | ||
| - | + | [[Категория:Прикладная статистика]] | |
| - | + | ||
Текущая версия
|
Критерий Уилкоксона (Вилкоксона) двухвыборочный — непараметрический статистический критерий, используемый для оценки различий между двумя выборками, взятыми из закона распределения, отличного от нормального, либо измеренными с использованием порядковой шкалы. Имеется аналог критерия Уилкоксона для связанных повторных наблюдений. Критерий является ранговым, поэтому он инвариантен по отношению к любому монотонному преобразованию шкалы измерения.
Пример задачи
Задача — сравнить две методики подготовки роженицы к родам. Сравнивается эффективность по оценке состояния новорожденного в баллах (шкала является порядковой).
Описание критерия
Заданы две выборки в противном случае следует поменять выборки местами.
Дополнительные предположения: обе выборки простые, объединённая выборка независима;
Вычисление статистики критерия:
- Построить общий вариационный ряд объединённой выборки
и найти ранги
всех элементов обеих выборок в общем вариационном ряду.
- Рассчитать суммы рангов, соответствующих обеим выборкам:
- Если размеры выборок совпадают (
), то значение статистики
будет равняется одной из сумм рангов
или
(любой). Если же выборки не равны, то
, то есть сумме рангов, соответствующей меньшей выборке. Заметим, что статистика
линейно связана со статистикой U-критерия Манна-Уитни.
Критерий (при уровне значимости ):
Против альтернативы :
- если
, то нулевая гипотеза отвергается. Здесь
есть
-квантиль табличного распределения Уилкоксона с параметрами
. [1][1]
Асимптотический критерий:
Рассмотрим нормированную и центрированную статистика Уилкоксона:
;
асимптотически имеет стандартное нормальное распределение. Нулевая гипотеза (против альтернативы
) отвергается, если
, где
есть
-квантиль стандартного нормального распределения.
Приближение можно использовать, если размер хотя бы одной из выборок превышает 25. Если размеры выборок равны, то данная аппроксимация хорошо работает до .[1]
Случай совпадающих наблюдений:
При наличии связок необходимо учесть их с помощью поправки. Выражение в знаменателе необходимо заменить на следующее:
- Здесь
- количество только тех связок, в которые входят ранги как одной, так и другой выборок,
- их размеры. Совпадения, целиком состоящие из элементов одной и той же выборки, на величину
не влияют. Наблюдения, не совпадающие с другими, рассматриваются как связки размера 1. Для элементов связок вычисляется средний ранг.
Поправка:[1]
В 1976 году Р. Иман предложил следующую аппроксимацию, обеспечивающую значительное снижение относительной ошибки для критических значений, в том числе на малых выборках. Поправка использует полусумму нормальной и стьюдентовской квантилей. Положим . Тогда:
.
Гипотеза отвергается, если
, где
обозначают соответственно квантили уровня
стандартного нормального распределения и распределения Стьюдента с
степенью свободы.
Применение критерия
В биологических и эконометрических приложениях метод часто используется для проверки гипотезы о равенстве средних двух независимых выборок. Вообще говоря, данное использование критерия некорректно. Можно построить примеры, когда , и средние выборок не совпадают.[1] При этом надо заметить, что данный недостаток не является редкостью, о многих популярных в математической статистике критериях можно сказать, что они не позволяют проверять те гипотезы, с которыми традиционно связаны. При применении подобных критериев к анализу реальных данных необходимо тщательно взвешивать их достоинства и недостатки.[1]
Критерий является аналогом критерия t-критерия Стьюдента для независимых выборок в случае закона распределения, отличного от нормального, либо данных, измеренных с использованием порядковой шкалы. Для нормально распределённых совокупностей следует использовать более мощный t-критерий.
Критерий Уилкоксона и U-критерий Манна-Уитни
Статистики критериев Уилкоксона и Уилкоксона-Манна-Уитни линейно связаны, поэтому, по сути, нет смысла говорить о двух различных критериях.[1] Оба они проверяют одну и ту же гипотезу и их границы применимости также совпадают. В то же время в литературе можно встретить рекомендации использовать критерий Уилкоксона для проверки равенства средних, когда нет предположений о дисперсиях,[1], а в случае равных дисперсий применять U-критерий Манна-Уитни.[1]
Проведём эксперимент: будем строить график достигаемого уровня значимости как функцию размера выборок и параметров распределения. Будем усреднять p-value по нескольким десяткам экспериментов.
Общие параметры для всех экспериментов:
- Выборки генерируются независимо из нормального распределения с заданными параметрами.
- Размер выборок варьируется от 50 до 500 с шагом 50.
- Значение p-value усредняется по 50 экспериментам.
- Размер выборки откладывается по вертикальной оси, переменный параметр по горизонтальной.
| Тип критерия | Параметры эксперимента | График |
|---|---|---|
| U-критерий Манна-Уитни | Среднее первой выборки: 0.
Среднее второй выборки: -3:0.3:3.[1] Дисперсия первой выборки: 5. Дисперсия второй выборки: 5. | 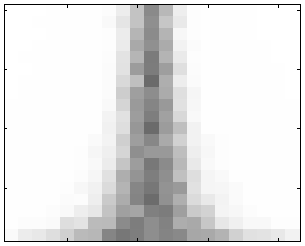
|
| Критерий Уилкоксона | Среднее первой выборки: 0.
Среднее второй выборки: -3:0.3:3. Дисперсия первой выборки: 5. Дисперсия второй выборки: 5. | 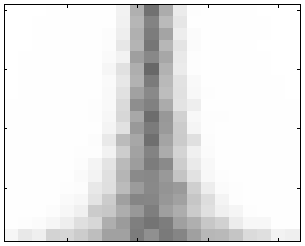
|
| U-критерий Манна-Уитни | Среднее первой выборки: 0.
Среднее второй выборки: -30:3:30. Дисперсия первой выборки: 1. Дисперсия второй выборки: 50. | 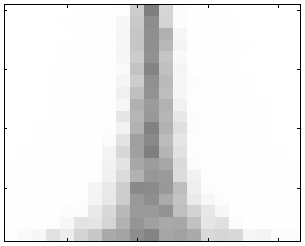
|
| Критерий Уилкоксона | Среднее первой выборки: 0.
Среднее второй выборки: -30:3:30. Дисперсия первой выборки: 1. Дисперсия второй выборки: 50. | 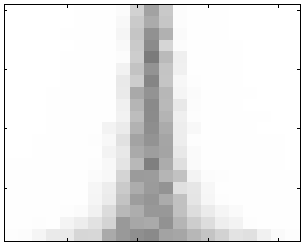
|
Легко видеть, что при одинаковых параметрах экспериментов графики p-value критериев Уилкоксона и Уилкоксона-Манна-Уитни практически совпадают, в том числе и в случае, когда дисперсии выборок существенно различаются.
Примечания
Литература
- Лагутин М. Б. Наглядная математическая статистика. В двух томах. — М.: П-центр, 2003. — 204-209 с.
- Лапач С. Н. , Чубенко А. В., Бабич П. Н. Статистика в науке и бизнесе. — Киев: Морион, 2002. — 160-164 с.
- Орлов А. И. Эконометрика. — М.: Экзамен, 2003. — §4.5.
- Кобзарь А. И. Прикладная математическая статистика. — М.: Физматлит, 2006. — 454-456 с.
Ссылки
- Критерий Уилкоксона-Манна-Уитни — аналогичный критерий.
- Проверка статистических гипотез — о методологии проверки статистических гипотез.
- Критерий Уилкоксона для связных выборок — аналог критерия для случая парных повторных наблюдений.


