Статистические свойства МНК-оценок коэффициентов регрессии

Материал из MachineLearning.

(Различия между версиями)

Версия 02:43, 29 января 2009

Статистическое исследование линейной регрессии включает в себя построение доверительных интервалов для коэффициентов регрессии и прогнозного значения отклика.

Однако прежде чем переходить к решению поставленной задачи, необходимо выяснить, какими статистическими свойствами обладают МНК-оценки коэффициентов регрессии.

Для того, чтобы регрессионная модель хорошо описывала исходные данные, а значит и МНК-оценки обладали хорошими свойствами, необходимо выполнение ряда предпосылок, называемых Основными Предположениями.

Содержание

1 Основные обозначения
2 Основные Предположения
3 Свойства МНК-оценок без предположения о нормальности
4 Свойства МНК-оценок с предположением о нормальности
5 Литература
6 См. также
7 Ссылки

Основные обозначения

Ввдедем матричные обозначения:

$X=$x_{11}\ \ \ldots\ \ x_{1k}<br>\ \vdots\ \ \ \ \ \ \ddots\ \ \ \ \vdots<br>x_{n1}\ \ \ldots\ \ x_{nk}$\;$ - матрица, столбцами которой являются векторы признаков (регрессоров), а строками - объекты;

$\hat{y}= \left[ \hat{y}_1 \\ ...\\ \hat{y}_n\right]$ – зависимая переменная (отклик);

$\theta= \left[\theta_1 \\ ...\\\theta_k \right]$ - коэффициенты линейной регрессии;

$\hat{y} = X\theta;$

$\varepsilon = y - \hat y \;$ - вектор регрессионных остатков.

Модель линейной регрессии имеет вид:

$y = X\theta + \varepsilon$

$\hat\theta = (X^TX)^{-1}X^Ty \;$ - МНК-оценка коэффициентов регрессии;

Основные Предположения

ОП.1 $X$ - детерминированная $n\times k$ матрица, $rkX = k$ (признаки линейно-независимы);
ОП.2 Регрессионные остатки $\varepsilon_i, \; i=\overline{1,n}$

2.1. одинаково распределены;

2.2. $E\varepsilon_i = 0$ (модель несмещенная);

2.3. $D\varepsilon_i = \sigma^2$ (гомоскедастичность);

2.4. $E\varepsilon_i\varepsilon_j = 0, \; i\neq j$ (некореллированность).

Дополнительное Предположение 3 (ДП3): $\; \; \varepsilon \sim N(0,\sigma^2I_n)$ ,

т.е вектор регрессионных остатков $\varepsilon$ - нормально распределенный случайный вектор со средним 0 и матрицей ковариации $\sigma^2I_n$ ( $I_n$ - единичная матрица размера $n\times n$ ). В этом случаем модель называется нормальной линейной регрессионной моделью.

Для проверки этих предположений используется Анализ регрессионных остатков.

Свойства МНК-оценок без предположения о нормальности

Теорема Гаусса-Маркова. Пусть выполнены ОП.1 и ОП.2. Тогда оценка $\hat\theta,$ полученная по методу наименьших квадратов является эффективной в классе линейных несмещенных оценок (Best Linear Unbiased Estimator, BLUE).

Исходя из этой теоремы можно выделить несколько основных свойств МНК-оценки $\hat\theta:$

Линейность:

$\hat\theta = Ay,$ где $A = (X^TX)^{-1}X^T;$

Несмещенность:

$E\hat\theta = E((X^TX)^{-1}X^Ty) = (X^TX)^{-1}X^TEy = (X^TX)^{-1}X^TE(X\theta+\varepsilon) = (X^TX)^{-1}X^TX\theta + (X^TX)^{-1}X^TE\varepsilon = \theta;$

Матрица ковариации равна:

$cov\hat\theta = ||cov(\hat\theta_i,\hat\theta_j)||_{i=1,\cdots,k}^{j=1,\cdots,k} = \sigma^2(X^TX)^{-1}.$

МНК-оценка $\hat\theta$ эффективна.

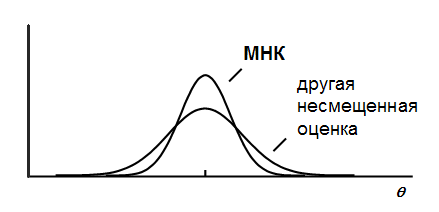
Итак, теорема Гаусса-Маркова утверждает, что любая другая линейная несмещенная оценка будет иметь большую дисперсию, чем МНК-оценка:

Нетрудно показать, что для любого вектора $\; c\in R^k \;$ оценка $\; c^T\hat\theta \;$ будет обладать теми же свойствами, что и МНК-оценка $\hat\theta$ . Поэтому:

если взять $c = (0\cdots 01\limits_j0\cdots0),$ то получим что

$c^T\hat\theta = \hat\theta_j$ - несмещенная, эффективная оценка $\theta_j;$

если $c = (x_{i1},\cdots,x_{ik}),$ то

$c^T\hat\theta = \hat y_i$ - несмещенная, эффективная оценка $y(x_i)_k.$

Свойства МНК-оценок с предположением о нормальности

Пусть теперь к тому же выполнено ДП3, т.е. $\varepsilon$ - многомерная нормально распределенная случайная величина, или, что то же самое $y_i$ имеют совместное нормальное распределение. Тогда к перечисленным выше свойствам добавятся следующие:

МНК-оценка коэффициентов регрессии $\hat\theta$ имеет нормальное распределение:

$\hat\theta \sim N(\theta, \sigma^2(X^TX)^{-1});$

Несмещенная оценка для дисперсии шума $\sigma^2$ имеет вид:

$\hat\sigma^2 = \frac{RSS}{n-k},$

где RSS есть остаточная сумма квадратов;

Случайная величина

$\frac{RSS}{\sigma^2} \sim \chi^2_{n-k}$

распределена по закону хи-квадрат с $n-k$ степенями свободы;

Оценки $\hat\theta$ и $s^2$ линейно независимы. Откуда получается, что величина

$\frac{\hat\theta-\theta}{\hat\sigma\sqrt{(X^TX)^{-1}}} \sim t_{n-k}$

имеет распределение Стьюдента с $n-k$ степенями свободы.

Литература

Кобзарь А. И. Прикладная математическая статистика. — М.: Физматлит, 2006.
Магнус Я. Р., Катышев П. К., Пересецкий А. А. Эконометрика. Начальный курс: Учеб. — 7-е изд., испр. — М.: Дело, 2005.

См. также

Ссылки

Источник — «http://machinelearning.ru/wiki/index.php?title=%D0%A1%D1%82%D0%B0%D1%82%D0%B8%D1%81%D1%82%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D0%B5_%D1%81%D0%B2%D0%BE%D0%B9%D1%81%D1%82%D0%B2%D0%B0_%D0%9C%D0%9D%D0%9A-%D0%BE%D1%86%D0%B5%D0%BD%D0%BE%D0%BA_%D0%BA%D0%BE%D1%8D%D1%84%D1%84%D0%B8%D1%86%D0%B8%D0%B5%D0%BD%D1%82%D0%BE%D0%B2_%D1%80%D0%B5%D0%B3%D1%80%D0%B5%D1%81%D1%81%D0%B8%D0%B8»

Категории: Прикладная статистика | Регрессионный анализ

@@ Строка 1: / Строка 1: @@
-Для того, чтобы '''[[метод наименьших квадратов|МНК-оценки]] коэффициентов [[многомерная линейная регрессия|многомерной регрессии]]''' обладали полезными '''статистическими свойствами''' необходимо выполнение ряда предпосылок относительно оцениваемой регрессионной модели, называемых ''Основными Положениями''.
+Статистическое исследование [[многомерная линейная регрессия|линейной регрессии]] включает в себя построение [[доверительный интервал|доверительных интервалов]] для коэффициентов регрессии и прогнозного значения отклика.
-==Основные Положения==
+Однако прежде чем переходить к решению поставленной задачи, необходимо выяснить, какими '''статистическими свойствами''' обладают '''[[Метод наименьших квадратов|МНК-оценки]] коэффициентов регрессии.'''
-*'''ОП.0''' <tex>Y = X\theta + \varepsilon</tex> (модель линейна по параметрам);
-*'''ОП.1''' <tex>X</tex> - детерминированная <tex>n\times k</tex> матрица, <tex>rkX = k</tex> (признаки линейно независимы);
+Для того, чтобы регрессионная модель хорошо описывала исходные данные, а значит и МНК-оценки обладали хорошими свойствами, необходимо выполнение ряда предпосылок, называемых ''Основными Предположениями''.
-*'''ОП.2''' Регрессионные остатки <tex>\varepsilon_i = y_i - \hat y_i = y_i - \sum\limits_{j=1}^k\theta_j x_{ij}, \; i=\overline{1,n}</tex>
+==Основные обозначения==
+Ввдедем матричные обозначения:
+*<tex>X=\(x_{11}\ \ \ldots\ \ x_{1k}<br>\ \vdots\ \ \ \ \ \ \ddots\ \ \ \ \vdots<br>x_{n1}\ \ \ldots\ \ x_{nk}\)\;</tex> - матрица, столбцами которой являются векторы признаков (регрессоров), а строками - объекты;
+*<tex> \hat{y}= \left[ \hat{y}_1 \\ ...\\ \hat{y}_n\right] </tex>  – зависимая переменная (отклик);
+*<tex> \theta= \left[\theta_1 \\ ...\\\theta_k  \right] </tex> - коэффициенты линейной регрессии;
+<tex> \hat{y} = X\theta;</tex>
+*<tex>\varepsilon = y - \hat y \; </tex> - вектор регрессионных остатков.
+Модель линейной регрессии имеет вид:
+::<tex>y = X\theta + \varepsilon</tex>
+* <tex>\hat\theta = (X^TX)^{-1}X^Ty \; </tex>- МНК-оценка коэффициентов регрессии;
+==Основные Предположения==
+*'''ОП.1''' <tex>X</tex> - детерминированная <tex>n\times k</tex> матрица, <tex>rkX = k</tex> (признаки линейно-независимы);
+*'''ОП.2''' Регрессионные остатки <tex>\varepsilon_i, \; i=\overline{1,n}</tex>
 ::'''2.1.''' одинаково распределены;
 ::'''2.2.''' <tex>E\varepsilon_i = 0</tex> (модель несмещенная);
 ::'''2.3.''' <tex>D\varepsilon_i = \sigma^2</tex> (гомоскедастичность);
 ::'''2.4.''' <tex>E\varepsilon_i\varepsilon_j = 0, \; i\neq j</tex> (некореллированность).
 *'''Дополнительное Предположение 3 (ДП3):''' <tex>\; \; \varepsilon \sim N(0,\sigma^2I_n)</tex>,
 :т.е вектор регрессионных остатков <tex>\varepsilon</tex> - [[нормальное распределение|нормально распределенный]] [[многомерная случайная величина|случайный вектор]] со [[многомерная случайная величина|средним]] 0 и [[ковариационная матрица|матрицей ковариации]] <tex>\sigma^2I_n</tex> (<tex>I_n</tex> - единичная матрица размера <tex>n\times n</tex>). В этом случаем модель называется ''нормальной линейной регрессионной моделью''.
+Для проверки этих предположений используется [[Анализ регрессионных остатков.]]
 ==Свойства МНК-оценок без предположения о нормальности==
-'''Теорема Гаусса-Маркова.''' Пусть выполнены основные положения 0-2. Тогда оценка <tex>\hat\theta,</tex> полученная по [[метод наименьших квадратов|методу наименьших квадратов]] является [[статистическое оценивание|эффективной]] в классе линейных (вида <tex>\hat\theta=Ay</tex>) [[статистическое оценивание|несмещенных]] оценок (Best Linear Unbiased Estimator, BLUE).
+'''Теорема Гаусса-Маркова.''' Пусть выполнены ОП.1 и ОП.2. Тогда оценка <tex>\hat\theta,</tex> полученная по [[метод наименьших квадратов|методу наименьших квадратов]] является [[статистическое оценивание|эффективной]] в классе линейных [[статистическое оценивание|несмещенных]] оценок (Best Linear Unbiased Estimator, BLUE).
 Исходя из этой теоремы можно выделить несколько основных '''свойств МНК-оценки <tex>\hat\theta:</tex>'''
@@ Строка 67: / Строка 93: @@
 [[Категория:Прикладная статистика]]
-[[Категория:Регрессианный анализ]]
+[[Категория:Регрессионный анализ]]

Статистические свойства МНК-оценок коэффициентов регрессии

Материал из MachineLearning.

Версия 02:43, 29 января 2009

Содержание

Основные обозначения

Основные Предположения

Свойства МНК-оценок без предположения о нормальности

Свойства МНК-оценок с предположением о нормальности

Литература

См. также

Ссылки

Просмотры

Личные инструменты

Навигация

Поиск

Инструменты