Исследование устойчивости оценок ковариационной матрицы параметров
Материал из MachineLearning.
Содержание |
Введение
В данной работе исследуется устойчивость оценок ковариационной матрицы параметров модели. Рассматриваются модели линейной регрессии. Тогда вектор параметров модели соответствует набору признаков модели. Ковариационная матрица параметров строится в предположении о вероятностном распределении вектора параметров. Исследуется, как будет меняться ковариационная матрица параметров модели при добавлении новых столбцов в матрицу плана. Для такой матрицы плана получаем расширенный вектор параметров модели и оценку матрицы ковариации параметров модели. Сравнивается ковариационная матрица для нерасширенного и расширенного вектора параметеров модели. Исследуется пространство параметров для информативных признаков.
Постановка задачи
Задана выборка .
Вектор свободных переменных
, зависимая переменная
.
Предполгается, что
где --- некоторая параметрическая функция,
--- вектор ее параметров,
--- ошибка, распределенная нормально с нулевым математическим ожиданием и дисперсией
,
. Предполагается, что вектор параметров
--- нормальнораспределенный случайный вектор с нулевым математическим ожиданием и матрицей ковариаций
.
Рассматривается класс линейных функций .
Наиболее вероятные параметры
имеют вид:
Для такого набора параметров исследуется матрица ковариации , который мы тоже оцениваем, используя принцип максимального правдоподобия.
Описание алгоритма оценки матрицы ковариации
Для фиксированных гиперпарамтеров ,
вектор наиболее вероятных параметров минимизирует функционал
Набор наиболее вероятных гиперпараметров будем искать, максимизируя оценку правдоподобия по ,
здесь --- гессиан функционала
.
В предположении о диагональности матрицы
и гессиана
,
,
, приравняв производные по гиперпараметрам к нулю, получаем оценку для
:
здесь .
Так же получаем оценку :
здесь
Используя оценки вектора параметров при фиксированных гиперпарамтерах и гиперпараметров при фиксированных параметрах, выпишем итерационный алгоритм поиска наиболее вероятных параметров и гиперпараметров. Он состоит из шагов:
- поиск вектора параметров, максимизирующих функционал
,
- поиск гиперпараметров, максимизирующих правдоподобие,
- проверка критерия остановки.
Критерий остановки --- малое изменение функционала для двух последовательных итераций алгоритма.
Вычислительный эксперимент
Один признак
В выборках один информативный признак и шумовых.
Вектор свободных переменных для каждого объекта генерируется из нормального распределения с нулевым математическим ожиданием и единичной дисперсией.
Рассматриваются выборки размером
и
.
Зависимая переменная --- зашумленная линейная или обобщенно-линейная функция входа.
Рассматривались обобщенные-линейные функции
и
.
Шум состоял из независимых нормальнораспределенных величин с дисперсией
.
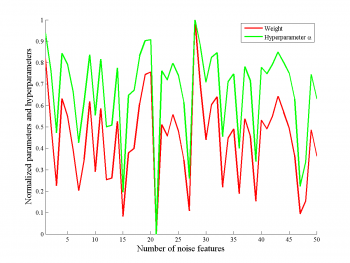
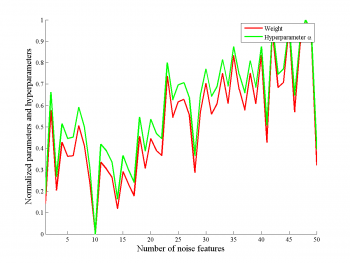
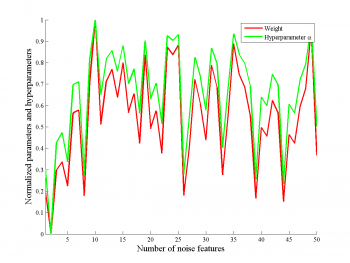
Зависимость параметра от гиперпараметров
На рисунках приведена зависимость параметра и гиперпараметра
, которые соответствуют нешумовому признаку.
Мы видим, что параметр сильно коррелирует с гиперпараметром, при этом, нет зависимости от числа шумовых признаков.
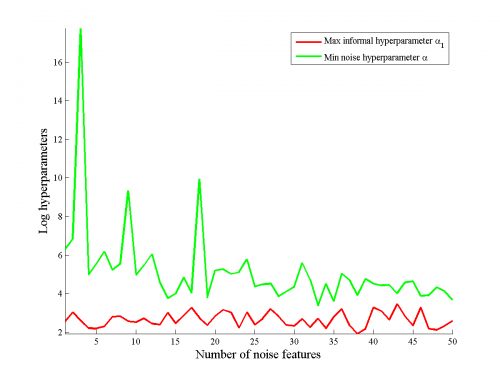
Сравнение гиперпараметров для разных признаков
Гиперпараметры могут служить мерой информативности признаков.
Сравнивались логарифм гиперпараметра значимого признака и минимальный из логарифмов гиперпарамтеров для незначимых признаков.
Бралось усреднение логарифма по пяти различным выборкам.
Результаты приведены на рисунках \ref{fig:hyperparametersCompare}.
На рисунке \ref{fig:hyperparametersCompare} видно, что в большинстве случаев значение гиперпараметра для значимого признака меньше, чем минимальное значение гиперпараметров для шумового, однако, в некоторых случаях наблюдаются выбросы.
Два признака
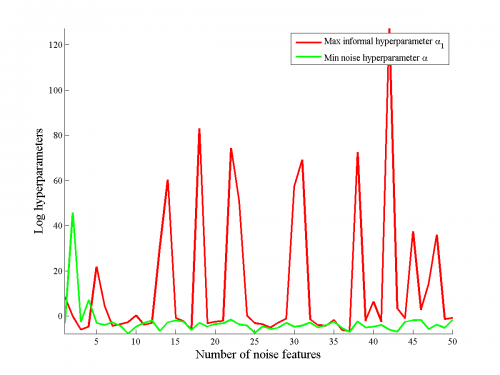
Проводился аналогичный эксперимент для двух информативных признаков, причем сравнивался максимальное значение гиперпараметра для информативных признаков с минимальным значением признака для шумовых признаков.
На рисунках \ref{fig:hyperparametersCompare2} видно, что информативные признаки имели меньшие значения гиперпараметра , чем информативные.
Таким образом, удается выделить информативные и шумовые признаки.
На рисунке \ref{fig:hyperparametersCompare3}показано сравнение информативности первого и второго информативных признаков, видно, что из-за большего веса один признак информативнее другого для линейной модели.
Так же отметим, что для обобщенно-линейной функции не удается выделить наиболее информативный признак, в некоторых случаях гиперпараметры для одного из признаков стремятся к бесконечности.
[Изображение:MeanAlphaVsNoiseAlpha2| Линейная функция] [Изображение:MeanAlphaVsNoiseAlpha2sin|Синусоида]
[Изображение:AlphasCompare|Линейная функция]
[Изображение:AlphasCompareSin|Синус]
Реальные данные
Использовались реальные данные по определения характеристик цемента по его составу.
Данные были нормализованы так, что как у свободных, так и у зависимой переменной были нулевые математические ожидания и единичные дисперсии.
Для данных без шумовых признаков алгоритм был запущен сто раз на разных подвыборках размера (размер полной выборки ---
).
Результаты приведены на рисунке \ref{fig:realDatanoNoise}.
Видно, что признаки разделяются по информативности и что информативность почти всегда эквивалента модулю веса.
Так же был проведен следующий эксперимент.
К начальному набору свободных переменных был добавлен ряд шумовых признаков, затем на ста запусках была оценена -процентная квантиль рассматриваемой величины.
На рисунке \ref{fig:realDataNoise} видно, что увеличение числа шумовых признаков увеличивает, хоть и не сильно, квантиль как оценки параметра, так и оценки гиперпараметра для разных признаков.
Отметим, что, тем не менее, это не влияет на разделимость признаков по информативности.
Выводы
Используемый подход устойчив по отношению к шумовым признакам, качество полученной аппроксимации и оценки весов и информативности для информативных признаков слабо зависят от количества шумовых признаков.
Исходный код и полный текст работы
Смотри также
Литература
- Стрижов В.В. и Сологуб Р.А. Алгоритм выбора нелинейных регрессионных моделей с анализом гиперпараметров. — ММРО-14. — 2009.
- Christopher M. Bishop Pattern Recognition and Machine Learning. — Hardcover. — 2006. — 740 с.
- Yeh, I. and others Modeling slump flow of concrete using second-order regressions and artificial neural networks. — 2007.
| | Данная статья является непроверенным учебным заданием.
До указанного срока статья не должна редактироваться другими участниками проекта MachineLearning.ru. По его окончании любой участник вправе исправить данную статью по своему усмотрению и удалить данное предупреждение, выводимое с помощью шаблона {{Задание}}. См. также методические указания по использованию Ресурса MachineLearning.ru в учебном процессе. |