Участник:Kropotov

Материал из MachineLearning.

Кропотов Дмитрий Александрович м.н.с. Вычислительного Центра РАН

Научные интересы

Байесовские методы машинного обучения, методы обучения и вывода в графических моделях, практический интеллектуальный анализ данных

Публикации

Список публикаций см. здесь.

Учебные курсы

Курс «Графические модели»
Спецкурс «Байесовские методы машинного обучения»
Спецсеминар «Байесовские методы машинного обучения»
Курс «Математические основы теории прогнозирования»

Программные реализации

Обобщенные линейные модели

Реализация под MatLab ряда классических алгоритмов решения задач классификации и регрессии на основе обобщенных линейных моделей, таких как байесовская линейная/логистическая регрессия, метод релевантных векторов и вариационный метод релевантных векторов. Эти алгоритмы просты в использовании и, как правило, обладают высокой скоростью работы. С их помощью можно решать задачи классификации и регрессии, а также осуществлять отбор значимых признаков. Скачать: glm V1.05 (RAR, 243 Кб)

Пример решения задачи регрессии: восстановление зашумленной функции sinc

Метод релевантных векторов для данных в виде многомерных массивов

Реализация под MatLab алгоритма решения задач классификации и регрессии, в которых каждый объект выборки представлен многомерным массивом признаков (в частности, матрицей признаков), и представляет интерес поиск информативных строк в этом многомерном массиве. Реализованный алгоритм — это вариационный метод релевантных векторов для табулярных данных, описанный в статье (Kropotov et al., 2010). Скачать: gridrvm V1.10 (RAR, 180 Кб)

Матрица признаков одного объекта

Только часть строк и столбцов матрицы являются информативными

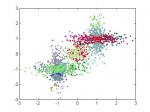
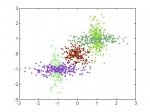
Смесь нормальных распределений

Реализация под MatLab алгоритмов решения задачи кластеризации с помощью восстановления смеси нормальных распределений с использованием EM-алгоритма, а также вариационного подхода, описанного в книге (Bishop, 2006). Количество кластеров может быть определено автоматически по данным с помощью скользящего контроля или с помощью подхода на основе автоматического определения релевантности, описанного в статье (Vetrov et al., 2010). Применение вариационного подхода для восстановления смеси нормальных распределений также позволяет автоматически определить число кластеров в данных. Скачать: gmm V1.10 (RAR, 102 Кб)

Пример кластеризации: начальное приближение с 20 кластерами

Пример кластеризации: финальная кластеризация на 5 кластеров

Реализации выполнены при поддержке РФФИ (проекты 09-01-12060, 09-01-92474).