Метод главных компонент

Материал из MachineLearning.

Перейти к: навигация, поиск

Метод Главных Компонент (англ. Principal Components Analysis, PCA) — один из основных способов уменьшить размерность данных, потеряв наименьшее количество информации. Изобретен К. Пирсоном (англ.Karl Pearson) в 1901 г. Применяется во многих областях, таких как распознавание образов, компьютерное зрение, сжатие данных и т. п. Вычисление главных компонент сводится к вычислению собственных векторов и собственных значений ковариационной матрицы исходных данных. Иногда метод главных компонент называют преобразованием Кархунена-Лоэва (англ. Karhunen-Loeve)[1] или преобразованием Хотеллинга (англ. Hotelling transform). Другие способы уменьшения размерности данных — это метод независимых компонент, многомерное шкалирование, а также многочисленные нелинейные обобщения: метод главных кривых и многообразий, поиск наилучшей проекции (англ. Projection Pursuit), нейросетевые методы «узкого горла», самоорганизующиеся карты Кохонена и др.

Содержание

Формальная постановка задачи

Статья в настоящий момент дорабатывается.
Agor153 03:21, 1 июля 2008 (MSD)



Задача анализа главных компонент, имеет, как минимум, три базовых версии:

  • аппроксимировать данные линейными многообразиями меньшей размерности;
  • найти подпространства меньшей размерности, в ортогональной проекции на которые разброс данных максимален;
  • для данной многомерной случайной величины построить такое ортогональное преобразования координат, что в результате корреляции между отдельными координатами обратятся в ноль.

Первые две версии оперируют конечными множествами данных. Они эквивалентны и не используют никакой гипотезы о статистическом порождении данных. Третья версия оперирует случайными величинами. Конечные множества появляются здесь как выборки из данного распределения, а решение двух первых задач — как приближение к «истинному» преобразованию Кархунена-Лоэва. При этом возникает дополнительный и не вполне тривиальный вопрос о точности этого приближения.

Аппроксимация данных линейными многообразиями

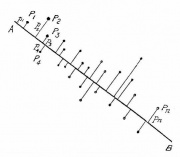
Иллюстрация к знаменитой работе К. Пирсона (1901): даны точки на плоскости, — расстояние от до прямой . Ищется прямая , минимизирующая сумму
Иллюстрация к знаменитой работе К. Пирсона (1901): даны точки P_i на плоскости, p_i — расстояние от P_i до прямой AB. Ищется прямая AB, минимизирующая сумму \sum_i p_i^2

Метод главных компонент начинался с задачи наилучшей аппроксимации конечного множества точек прямыми и плоскостями (К. Пирсон, 1901). Дано конечное множество векторов x_1,x_2,...x_m \in\mathbb{R}^n . Для каждого k = 0,1,..., n-1 среди всех k-мерных линейных многообразий в \mathbb{R}^n найти такое L_k \subset \mathbb{R}^n , что сумма квадратов уклонений x_i от L_k минимальна:

\sum_{i=1}^m \operatorname{dist}^2(x_i, L_k) \to \min,

где \operatorname{dist}(x_i, L_k) — евклидово расстояние от точки до линейного многообразия. Всякое k -мерное линейное многообразие в \mathbb{R}^n может быть задано как множество линейных комбинаций L_k = \{ a_0 +\beta_1 a_1 +...+ \beta_k a_k | \beta_i \in \mathbb{R} \} , где параметры \beta_i пробегают вещественную прямую \mathbb{R}, a_0 \in \mathbb{R}^n а \left\{a_1,..., a_k \right\} \subset \mathbb{R}^n — ортонормированный набор векторов

\operatorname{dist}^2(x_i, L_k) = \| x_i - a_0 - \sum_{j=1}^k a_j (a_j, x_i - a_0) \| ^2,

где \| \cdot \| евклидова норма, \left(a_j, x_i\right) — евклидово скалярное произведение, или в координатной форме:

\operatorname{dist}^2(x_i, L_k) = \sum_{l=1}^n \left(x_{il} - a_{0l}- \sum_{j=1}^k a_{jl} \sum_{q=1}^n a_{jq}(x_{iq} - a_{0q}) \right)^2 .

Решение задачи аппроксимации для k = 0,1,..., n-1 даётся набором вложенных линейных многообразий L_0 \subset L_1 \subset ... L_{n-1} , L_k = \{ a_0 +\beta_1 a_1 +...+ \beta_k a_k | \beta_i \in \mathbb{R} \} . Эти линейные многообразия определяются ортонормированным набором векторов \left\{a_1,..., a_{n-1} \right\} (векторами главных компонент) и вектором a_0 . Вектор a_0 ищется, как решение задачи минимизации для L_0 :

a_0 = \underset{a_0\in\mathbb{R}^n}{\operatorname{argmin}} \left(\sum_{i=1}^m \operatorname{dist}^2(x_i, L_0)\right),

то есть

a_0 = \underset{a_0\in\mathbb{R}^n}{\operatorname{argmin}} \left (\sum_{i=1}^m \| x_i - a_0\| ^2\right) .

Это — выборочное среднее: a_0 = \frac{1}{m} \sum_{i=1}^m x_i = \overline{X}. Фреше в 1948 году обратил внимание, что вариационное определение среднего (как точки, минимизирующей сумму квадратов расстояний до точек данных) очень удобно для построения статистики в произвольном метрическом пространстве, и построил обобщение классической статистики для общих пространств (обобщённый метод наименьших квадратов).

Векторы главных компонент могут быть найдены как решения однотипных задач оптимизации:

1) централизуем данные (вычитаем среднее): x_i:= x_i - \overline{X_i}. Теперь \sum_{i=1}^m x_i =0 ;
2) находим первую главную компоненту как решение задачи;
a_1 = \underset{\| a_1 \| =1}{\operatorname{argmin}} \left( \sum_{i=1}^m \| x_i - a_1 (a_1,x_i)\| ^2\right).
Если решение не единственно, то выбираем одно из них.
3) Вычитаем из данных проекцию на первую главную компоненту:
x_i:= x_i - a_1 \left(a_1,x_i\right) ;
4) находим вторую главную компоненту как решение задачи
a_2 = \underset{\| a_2 \| =1}{\operatorname{argmin}} \left( \sum_{i=1}^m \| x_i - a_2 (a_2,x_i)\| ^2\right) .
Если решение не единственно, то выбираем одно из них.
…
2k-1) Вычитаем проекцию на (k-1)-ю главную компоненту (напомним, что проекции на предшествующие (k-2) главные компоненты уже вычтены):
x_i:= x_i - a_{k-1} \left(a_{k-1},x_i\right) ;
2k) находим k-ю главную компоненту как решение задачи:
a_k = \underset{\| a_k \| =1}{\operatorname{argmin}} \left( \sum_{i=1}^m \| x_i - a_k (a_k,x_i)\| ^2\right) .
Если решение не единственно, то выбираем одно из них.
…

На каждом подготовительном шаге (2k-1) вычитаем проекцию на предшествующую главную компоненту. Найденные векторы \left\{a_1,..., a_{ n -1} \right\} ортонормированы просто в результате решения описанной задачи оптимизации, однако чтобы не дать ошибкам вычисления нарушить взаимную ортогональность векторов главных компонент, можно включать a_k \bot \{a_1,..., a_{k -1} \} в условия задачи оптимизации.

Неединственность в определении a_k помимо тривиального произвола в выборе знака ( a_k и -a_k решают ту же задачу) может быть более существенной и происходить, например, из условий симметрии данных.

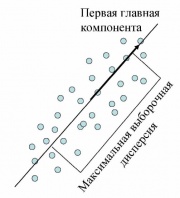
Поиск ортогональных проекций с наибольшим рассеянием

Первая главная компонента максимизирует выборочную дисперсию проекции данных
Первая главная компонента максимизирует выборочную дисперсию проекции данных


Пусть нам дан центрированный набор векторов данных x_i\in\mathbb{R}^n \; (i=1,...,m) (среднее арифметическое значение x_i равно нулю). Задача — найти такое ортогональное преобразование в новую систему координат, для которого были бы верны следующие условия:

  • Выборочная дисперсия данных вдоль первой координаты максимальна (эту координату называют первой главной компонентой);
  • Выборочная дисперсия данных вдоль второй координаты максимальна при условии ортогональности первой координате (вторая главная компонента);
  • …
  • Выборочная дисперсия данных вдоль значений k-ой координаты максимальна при условии ортогональности первым k-1 координатам;
  • …

Выборочная дисперсия данных вдоль направления, заданного нормированным вектором a_k, это

S^2_m \left[ (X, a_k) \right ] = \frac{1}{m} \sum\limits_{i=1}^m \left(\sum\limits_{j=1}^n x_{ij}a_{kj} \right)^2

(поскольку данные центрированы, выборочная дисперсия здесь совпадает со средним квадратом уклонения от нуля).

Формально, если A=\left \{a_1,...,a_n \right \}^T\in\mathbb{R}^{n \times n}, a_k\in\mathbb{R}^n — искомое преобразование, то для векторов a_k должны выполняться следующие условия:

  • a_1 = \underset{\| a_1 \| =1}{\operatorname{argmax}}\,S^2_m \left [(X, a_1) \right ];
Если решение не единственно, то выбираем одно из них.
  • Вычитаем из данных проекцию на первую главную компоненту:
x_i:= x_i - a_1 \left(a_1,x_i\right) ; в результате x_i \bot a_1;
  • находим вторую главную компоненту как решение задачи
a_2 = \underset{\| a_2 \| =1}{\operatorname{argmax}}\,S^2_m \left [ (X, a_2) \right ];
Если решение не единственно, то выбираем одно из них.
  • …
  • Вычитаем проекцию на (k-1)-ю главную компоненту (напомним, что проекции на предшествующие k-2 главные компоненты уже вычтены):
x_i:= x_i - a_{k-1} \left(a_{k-1},x_i\right) ; в результате x_i \bot a_l, (l = 1, \dots, k-1);
  • находим k-ю главную компоненту как решение задачи
a_n = \underset{\| a_k\| = 1}{\operatorname{argmax}}\,S^2_m \left [ (X, a_k) \right ];
Если решение не единственно, то выбираем одно из них.
  • …

Фактически, как и для задачи аппроксимации, на каждом шаге решается задача о первой главной компоненте для данных, из которых вычтены проекции на все ранее найденные главные компоненты. При большом числе итерации (большая размерность, много главных компонент) отклонения от ортогональности накапливаются и может потребоваться специальная коррекция алгоритма или другой алгоритм поиска собственных векторов ковариационной матрицы.

Решение задачи о наилучшей аппроксимации даёт то же множество решений \left\{a_i\right\}, что и поиск ортогональных проекций с наибольшим рассеянием, по очень простой причине: \| x_i - a_k (a_k,x_i)\| ^2 = \| x_i\| ^2 - (a_k,x_i)^2, и первое слагаемое не зависит от a_k. Только одно дополнение к задаче об аппроксимации: появляется последняя главная компонента a_n.

Поиск ортогональных проекций с наибольшим среднеквадратичным расстоянием между точками

Ещё одна эквивалентная формулировка следует из очевидного тождества, верного для любых m векторов x_i:

\frac{1}{m(m-1)}\sum_{i,j=1}^m (x_i-x_j)^2 =\frac{2m^2}{m(m-1)}\left[\frac{1}{m}\sum_{i=1}^m x_i^2 - \left(\frac{1}{m}\sum_{i}^m x_i \right)^2\right].

В левой части этого тождества стоит среднеквадратичное расстояние между точками, а в квадратных скобках справа — выборочная дисперсия. Таким образом, в методе главных компонент ищутся подпространства, в проекции на которые среднеквадратичное расстояние между точками максимально. Такая переформулировка позволяет строить обобщения с взвешиванием различных парных расстояний (а не только точек).

Аннулирование корреляций между координатами

Для заданной n-мерной случайной величины X найти такой ортонормированный базис, \left\{a_1,..., a_n \right\}, в котором коэффициент ковариации между различными координатами равен нулю. После преобразования к этому базису

\operatorname{cov}(X_i,X_j)=0 для i \neq j .

Здесь \operatorname{cov}(X_i,X_j)= \operatorname{E}[(X_i-\overline{X_i})(X_j-\overline{X_j})] — коэффициент ковариации.

Диагонализация ковариационной матрицы

Все задачи о главных компонентах приводят к задаче диагонализации ковариационной матрицы или выборочной ковариационной матрицы. Эмпирическая или выборочная ковариационная матрица, это

C = [c_{ij}],\ c_{ij} = \frac{1}{m} \sum_{l=1}^m (x_{li}-\overline{X_{i}})(x_{lj}-\overline{X_{j}}).

Ковариационная матрица многомерной случайной величины X, это

\Sigma = [\sigma_{ij}],\ \sigma_{ij} = \operatorname{cov}(X_i,X_j)=E[(X_i-\overline{X_i})(X_j-\overline{X_j})].

Векторы главных компонент для задач о наилучшей аппроксимации и о поиске ортогональных проекций с наибольшим рассеянием — это ортонормированный набор \left\{a_1,..., a_n \right\} собственных векторов эмпирической ковариационной матрицы C, расположенных в порядке убывания собственных значений \lambda: \lambda_1 \ge \lambda_2 \ge ... \ge \lambda_n \ge 0. Эти векторы служат оценкой для собственных векторов ковариационной матрицы \operatorname{cov}(X_i,X_j) . В базисе из собственных векторов ковариационной матрицы она, естественно, диагональна, и в этом базисе коэффициент ковариации между различными координатами равен нулю.

Если спектр ковариационной матрицы вырожден, то выбирают произвольный ортонормированный базис собственных векторов. Он существует всегда, а собственные числа ковариационной матрицы всегда вещественны и неотрицательны.

Сингулярное разложение матрицы данных

Идея сингулярного разложения

Математическое содержание метода главных компонент — это спектральное разложение ковариационной матрицы C , то есть представление пространства данных в виде суммы взаимно ортогональных собственных подпространств C , а самой матрицы C — в виде линейной комбинации ортогональных проекторов на эти подпространства с коэффициентами \lambda_i . Если \operatorname{X}=\left\{x_1,..., x_m \right\}^T — матрица, составленная из векторов-строк центрированных данных, то C = \operatorname{X}^T\operatorname{X} и задача о спектральном разложении ковариационной матрицы C превращается в задачу о сингулярном разложении (англ. Singular value decomposition) матрицы данных \operatorname{X}.

Число \sigma \geq 0 называется сингулярным числом матрицы \operatorname{X} тогда и только тогда, когда существуют правый и левый сингулярные векторы: такие m-мерный вектор-строка b_{\sigma} и n-мерный вектор-столбец a_{\sigma} (оба единичной длины), что выполнено два равенства:

\operatorname{X} a_{\sigma} = \sigma b_{\sigma}^T \;;\, \, b_{\sigma} \operatorname{X}= \sigma a_{\sigma}^T.

Пусть p= \operatorname{rang} \operatorname{X} \leq \min\{n,m\} — ранг матрицы данных. Сингулярное разложение матрицы данных \operatorname{X} — это её представление в виде

\operatorname{X}= \sum_{l=1}^p \sigma_l b_l^T a_l^T \;; \;\operatorname{X}^T= \sum_{l=1}^p \sigma_l a_l b_l \; \left(x_{ij}=\sum_{l=1}^p \sigma_l b_{li}a_{lj}\right),

где \sigma_l > 0 — сингулярное число, a_l=(a_{li}), \, i=1,... n — соответствующий правый сингулярный вектор-столбец, а b_l=(b_{li}), \, i=1,... m — соответствующий левый сингулярный вектор-строка (l=1,...p). Правые сингулярные векторы-столбцы a_l, участвующие в этом разложении, являются векторами главных компонент и собственными векторами эмпирической ковариационной матрицы C =\operatorname{X} ^T \operatorname{X} , отвечающими положительным собственным числам \lambda_l=\sigma_l^2 > 0 .

Хотя формально задачи сингулярного разложения матрицы данных и спектрального разложения ковариационной матрицы совпадают, алгоритмы вычисления сингулярного разложения напрямую, без вычисления спектра ковариационной матрицы, более эффективны и устойчивы [1].

Теория сингулярного разложения была создана Дж. Дж. Сильвестром (англ.J. J. Sylvester}}) в 1889 г. и изложена во всех подробных руководствах по теории матриц [1].

Простой итерационный алгоритм сингулярного разложения

Основная процедура — поиск наилучшего приближения произвольной m \times n матрицы X=(x_{ij}) матрицей вида b \otimes a = (b_i a_j) (где b — m-мерный вектор, а a — n-мерный вектор) методом наименьших квадратов:

F(b, a) = \frac{1}{2}\sum_{i=1}^m \sum_{j=1}^n (x_{ij} - b_i a_j )^2 \to \min

Решение этой задачи дается последовательными итерациями по явным формулам. При фиксированном векторе a=(a_j) значения b=(b_i) , доставляющие минимум форме F(b, a) , однозначно и явно определяются из равенств \partial F/ \partial b_i = 0 :

\frac{\partial F}{\partial b_i} = - \sum_{j=1}^n (x_{ij} - b_i a_j )a_j = 0; \;\; b_i = \frac{\sum_{j=1}^n x_{ij} a_j}{\sum_{j=1}^n a_j^2 }\, .

Аналогично, при фиксированном векторе b =(b_ i) определяются значения a=(a_j) :

a_j = \frac{\sum_{i=1}^m b_i x_{ij} }{\sum_{i =1}^m b_i ^2 }\, .

B качестве начального приближения вектора a возьмем случайный вектор единичной длины, вычисляем вектор b, далее для этого вектора b вычисляем вектор a и т. д. Каждый шаг уменьшает значение F(b, a) . В качестве критерия остановки используется малость относительного уменьшения значения минимизируемого функционала F(b, a) за шаг итерации (\Delta F / F ) или малость самого значения F.

В результате для матрицы X=(x_{ij}) получили наилучшее приближение матрицей P_1 вида b^1 \otimes a^1 = (b_i^1 a_j^1) (здесь верхним индексом обозначен номер итерации). Далее, из матрицы X вычитаем полученную матрицу P_1, и для полученной матрицы уклонений X_1=X-P_1 вновь ищем наилучшее приближение P_2 этого же вида и т. д., пока, например, норма X_k не станет достаточно малой. В результате получили итерационную процедуру разложения матрицы X в виде суммы матриц ранга 1, то есть X=P_1+P_2+... +P_q \; (P_l = b^l \otimes a^l) . Полагаем \sigma_l = \|a^l\| \|b^l\| и нормируем векторы a^l \, , \, b^l: a^l:= a^l/ \| a^l\|; \, \, b^l:= b^l/ \| b^l\|. В результате получена аппроксимация сингулярных чисел \sigma_l и сингулярных векторов (правых — a^l и левых — b^l).

К достоинствам этого алгоритма относится его исключительная простота и возможность почти без изменений перенести его на данные с пробелами[1], а также взвешенные данные.

Существуют различные модификации базового алгоритма, улучшающие точность и устойчивость. Например, векторы главных компонент a^l при разных l должны быть ортогональны «по построению», однако при большом числе итерации (большая размерность, много компонент) малые отклонения от ортогональности накапливаются и может потребоваться специальная коррекция a^l на каждом шаге, обеспечивающая его ортогональность ранее найденным главным компонентам.

Для квадратных симметричных положительно определённых матриц описанный алгоритм превращается в метод прямых итераций для поиска собственных векторов (см. статью Собственные векторы, значения и пространства).

Матрица преобразования к главным компонентам

Матрица A преобразования данных к главным компонентам строится из векторов главных компонент: A=\left \{a_1,...,a_n \right \}^T. Здесь a_i — ортонормированные векторы-столбцы главных компонент, расположенные в порядке убывания собственных значений, верхний индекс T означает транспонирование. Матрица A является ортогональной: A A^T=1.

После преобразования большая часть вариации данных будет сосредоточена в первых координатах, что даёт возможность отбросить оставшиеся и рассмотреть пространство уменьшенной размерности.

Остаточная дисперсия

Пусть данные центрированы, \overline{ X}=0. При замене векторов данных x_i на их проекцию на первые k главных компонент x_i \mapsto \sum_{j=1}^k a_j (a_j, x_i) вносится средний квадрат ошибки в расчете на один вектор данных:

\frac{1}{m} \sum_{i=1}^m \left\| x_i - \sum_{j=1}^k a_j (a_j, x_i) \right \| ^2=\sum_{l=k+1}^n \lambda_l,

где \lambda_1 \ge \lambda_2 \ge ... \ge \lambda_n \ge 0 собственные значения эмпирической ковариационной матрицы C, расположенные в порядке убывания, с учетом кратности.

Эта величина называется остаточной дисперсией. Величина

\frac{1}{m} \sum_{i=1}^m \left\| \sum_{j=1}^k a_j (a_j, x_i) \right\| ^2=\frac{1}{m} \sum_{i=1}^m \sum_{j=1}^k (a_j, x_i)^2=\sum_{l=1}^k \lambda_l

называется объяснённой дисперсией. Их сумма равна выборочной дисперсии. Соответствующий квадрат относительной ошибки — это отношение остаточной дисперсии к выборочной дисперсии (то есть доля необъяснённой дисперсии):

\delta^2_k=\frac{\lambda_{k+1}+\lambda_{k+2}+...+\lambda_{n}}{\lambda_{1}+\lambda_{2}+...+\lambda_{n}}.

По относительной ошибке \delta_k оценивается применимость метода главных компонент с проецированием на первые k компонент.

Замечание: в большинстве вычислительных алгоритмов собственные числа \lambda_i с соответствуюшими собственными векторами — главными компонентами a_i вычисляются в порядке «от больших \lambda_i — к меньшим». Для вычисления \delta_k достаточно вычислить первые k собственных чисел и след эмпирической ковариационной матрицы C, \operatorname{tr} C (сумму диагональных элементов C, то есть дисперсий по осям). Тогда

\delta^2_k=\frac{1}{\operatorname{tr} C}\left(\operatorname{tr} C -\sum_{i=1}^k \lambda_{i}\right).

Нормировка

Нормировка после приведения к главным компонентам

После проецирования на первые k главных компонент с \lambda_1 \ge \lambda_2 \ge ... \ge \lambda_k > 0 удобно произвести нормировку на единичную (выборочную) дисперсию по осям. Дисперсия вдоль iй главной компоненты равна \lambda_i > 0 \; (1 \le i \le k), поэтому для нормировки надо разделить соответствующую координату на \sqrt{ \lambda_i}. Это преобразование не является ортогональным и не сохраняет скалярного произведения. Ковариационная матрица проекции данных после нормировки становится единичной, проекции на любые два ортогональных направления становятся независимыми величинами, а любой ортонормированный базис становится базисом главных компонент (напомним, что нормировка меняет отношение ортогональности векторов). Отображение из пространства исходных данных на первые k главных компонент вместе с нормировкой задается матрицей

K=\left \{\frac{a_1}{\sqrt{ \lambda_1}},\frac{a_2}{\sqrt{ \lambda_2}},...,\frac{a_k}{\sqrt{ \lambda_k}} \right \}^T.

Именно это преобразование чаще всего называется преобразованием Кархунена-Лоэва. Здесь a_i — векторы-столбцы, а верхний индекс T означает транспонирование.

Нормировка до вычисления главных компонент

Предупреждение: не следует путать нормировку, проводимую после преобразования к главным компонентам, с нормировкой и «обезразмериванием» при предобработке данных, проводимой до вычисления главных компонент. Предварительная нормировка нужна для обоснованного выбора метрики, в которой будет вычисляться наилучшая аппроксимация денных, или будут искаться направления наибольшего разброса (что эквивалентно). Например, если данные представляют собой трёхмерные векторы из «метров, литров и килограмм», то при использовании стандартного евклидового расстояния разница в 1 метр по первой координате будет вносить тот же вклад, что разница в 1 литр по второй, или в 1 кг по третьей. Обычно системы единиц, в которых представлены исходные данные, недостаточно точно отображают наши представления о естественных масштабах по осям, и проводится «обезразмеривание»: каждая координата делится на некоторый масштаб, определяемый данными, целями их обработки и процессами измерения и сбора данных.

Есть три cущественно различных стандартных подхода к такой нормировке: на единичную дисперсию по осям (масштабы по осям равны средним квадратичным уклонениям — после этого преобразования ковариационная матрица совпадает с матрицей коэффициентов корреляции), на равную точность измерения (масштаб по оси пропорционален точности измерения данной величины) и на равные требования в задаче (масштаб по оси определяется требуемой точностью прогноза данной величины или допустимым её искажением — уровнем толерантности). На выбор предобработки влияют содержательная постановка задачи, а также условия сбора данных (например, если коллекция данных принципиально не завершена и данные будут ещё поступать, то нерационально выбирать нормировку строго на единичную дисперсию, даже если это соответствует смыслу задачи, поскольку это предполагает перенормировку всех данных после получения новой порции; разумнее выбрать некоторый масштаб, грубо оценивающий стандартное отклонение, и далее его не менять).

Предварительная нормировка на единичную дисперсию по осям разрушается поворотом системы координат, если оси не являются главными компонентами, и нормировка при предобработке данных не заменяет нормировку после приведения к главным компонентам.

Механическая аналогия и метод главных компонент для взвешенных данных

Если сопоставить каждому вектору данных единичную массу, то эмпирическая ковариационная матрица C совпадёт с тензором инерции этой системы точечных масс (делённым на полную массу m), а задача о главных компонентых — с задачей приведения тензора инерции к главным осям. Можно использовать дополнительную свободу в выборе значений масс для учета важности точек данных или надежности их значений (важным данным или данным из более надежных источников приписываются бо́льшие массы). Если вектору данных x_l придаётся масса w_l, то вместо эмпирической ковариационной матрицы C получим

C^w = [c^w_{ij}],\ c^w_{ij} = \frac{1}{\sum_{l} w_l} \sum_{l=1}^m w_l(x_{li}-\overline{X_{i}})(x_{lj}-\overline{X_{j}}).

Все дальнейшие операции по приведению к главным компонентам производятся так же, как и в основной версии метода: ищем ортонормированный собственный базис C^w, упорядочиваем его по убыванию собственных значений, оцениваем средневзвешенную ошибку аппроксимации данных первыми k компонентами (по суммам собственных чисел C^w), нормируем и т. п.

Более общий способ взвешивания даёт максимизация взвешенной суммы попарных расстояний[1] между проекциями. Для каждых двух точек данных, x_l , \ x_q вводится вес d_{lq}; d_{lq}=d_{ql} и d_{l}=\sum_{q=1}^m d_{lq}. Вместо эмпирической ковариационной матрицы C используется

C^d = [c^d_{ij}],\ c^d_{ij} =\sum_{l=1}^m d_l (x_{li}-\overline{X_{i}})(x_{lj}-\overline{X_{j}}) -\sum_{l \neq q, \ l,q=1}^m d_{lq}(x_{li} - \overline{X_{i}})(x_{qj}- \overline{X_{j}}).

При d_{lq}>0 симметричная матрица C^d положительно определена, поскольку положительна квадратичная форма:

\sum_{ij} c^d_{ij}a_i a_j = \frac{1}{2}\sum_{lq}d_{lq}\left(\sum_ia_i(x_{li}-x_{qi})\right)^2.

Далее ищем ортонормированный собственный базис C^d, упорядочиваем его по убыванию собственных значений, оцениваем средневзвешенную ошибку аппроксимации данных первыми k компонентами и т. д. — в точности так же, как и в основном алгоритме.

Этот способ применяется при наличии классов: для x_l , \ x_q из разных классов вес d_{lq} вес выбирается бо́льшим, чем для точек одного класса. В результате, в проекции на взвешенные главные компоненты различные классы «раздвигаются» на большее расстояние.

Другое применение — снижение влияния больших уклонений (оутлайеров, англ.Outlier), которые могут искажать картину из-за использования среднеквадратичного расстояния: если выбрать d_{lq}=1/ \| x_l -x_q \|, то влияние больших уклонений будет уменьшено. Таким образом, описанная модификация метода главных компонент является более робастной, чем классическая.

Устойчивость главных компонент

Специальная терминология

В статистике при использовании метода главных компонент используют несколько специальных терминов.

Матрица данных \mathbf{X}=\{x_1,... x_m\}^T; каждая строка — вектор предобработанных данных (центрированных и правильно нормированных), число строк — m (количество векторов данных), число столбцов — n (размерность пространства данных);

Матрица нагрузок (Loadings) \mathbf{P}=\{a_1,... a_k\}; каждый столбец — вектор главных компонент, число строк — n (размерность пространства данных), число столбцов — k (количество векторов главных компонент, выбранных для проецирования);

Матрица счетов (Scores) \mathbf{T}=[t_{ij}]; \; t_{ij}=(x_i,a_j); каждая строка — проекция вектора данных на k главных компонент; число строк — m (количество векторов данных), число столбцов — k (количество векторов главных компонент, выбранных для проецирования);

Матрица Z-счетов (Z-scores) \mathbf{Z}=[z_{ij}]; \; z_{ij}=\frac{(x_i,a_j)}{\sqrt{ \lambda_j}}; каждая строка — проекция вектора данных на k главных компонент, нормированная на единичную выборочную дисперсию; число строк — m (количество векторов данных), число столбцов — k (количество векторов главных компонент, выбранных для проецирования);

Матрица ошибок (или остатков) (Errors or residuals) \mathbf{E}=\mathbf{X}-\mathbf{T}\mathbf{P}^T.

Основная формула: \mathbf{X}=\mathbf{T}\mathbf{P}^T+\mathbf{E}.

Пределы применимости и ограничения эффективности метода

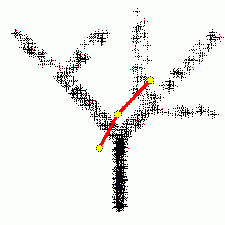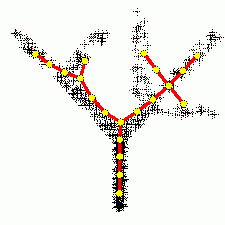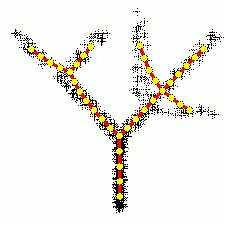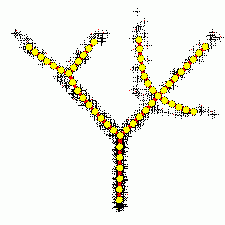
Построение ветвящихся главных компонент методом топологических грамматик. Крестики — точки данных, красное дерево с желтыми узлами — аппроксимирующий дендрит.
Построение ветвящихся главных компонент методом топологических грамматик. Крестики — точки данных, красное дерево с желтыми узлами — аппроксимирующий дендрит[1].

Метод главных компонент применим всегда. Распространённое утверждение о том, что он применим только к нормально распределённым данным (или для распределений, близких к нормальным) неверно: в исходной формулировке К. Пирсона ставится задача об аппроксимации конечного множества данных и отсутствует даже гипотеза о их статистическом порождении, не говоря уж о распределении.

Однако метод не всегда эффективно снижает размерность при заданных ограничениях на точность \delta_k. Прямые и плоскости не всегда обеспечивают хорошую аппроксимацию. Например, данные могут с хорошей точностью следовать какой-нибудь кривой, а эта кривая может быть сложно расположена в пространстве данных. В этом случае метод главных компонент для приемлемой точности потребует нескольких компонент (вместо одной), или вообще не даст снижения размерности при приемлемой точности. Для работы с такими «кривыми» главными компонентами изобретен метод главных многообразий[1] и различные версии нелинейного метода главных компонент[1][1]. Больше неприятностей могут доставить данные сложной топологии. Для их аппроксимации также изобретены различные методы, например самоорганизующиеся карты Кохонена, нейронный газ[1] или топологические грамматики[1]. Если данные статистически порождены с распределением, сильно отличающимся от нормального, то для аппроксимации распределения полезно перейти от главных компонент к независимым компонентам[1], которые уже не ортогональны в исходном скалярном произведении. Наконец, для изотропного распределения (даже нормального) вместо эллипсоида рассеяния получаем шар, и уменьшить размерность методами аппроксимации невозможно.

Примеры использования

Компрессия изображений и видео

Для уменьшения пространственной избыточности пикселей при кодировании изображений и видео используется линейные преобразования блоков пикселей. Последующие квантования полученных коэффициентов и кодирование без потерь позволяют получить значительные коэффициенты сжатия. Использование преобразования PCA в качестве линейного преобразования является для некоторых типов данных оптимальным с точки зрения размера полученных данных при одинаковом искажении [1]. На данный момент этот метод активно не используется, в основном из-за большой вычислительной сложности. Также сжатия данных можно достичь отбрасывая последние коэффициенты преобразования.

Подавление шума на изображениях [1]

Основная суть метода — при удалении шума из блока пикселей представить окрестность этого блока в виде набора точек в многомерном пространстве, применить к нему PCA и оставить только первые компоненты преобразования. При этом предполагается, что в первых компонентах содержится основная полезная информация, оставшиеся же компоненты содержат ненужный шум. Применив обратное преобразование после редукции базиса главных компонент, мы получим изображение без шума.

Индексация видео

Основная идея — представить при помощи PCA каждый кадр видео несколькими значениями, которые в дальнейшем будут использоваться при построении базы данных и запросам к ней. Столь существенная редукция данных позволяет значительно увеличить скорость работы и устойчивость к ряду искажений в видео.

Биоинформатика

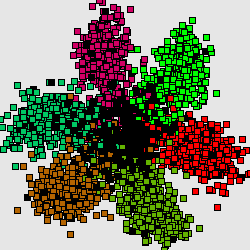
Рис. А. Проекция ДНК-блуждания на первые 2 главные компоненты для генома бактерии Streptomyces coelicolor
Рис. А. Проекция ДНК-блуждания на первые 2 главные компоненты для генома бактерии Streptomyces coelicolor
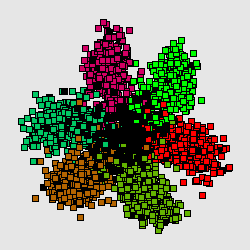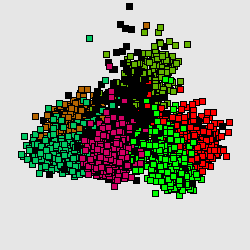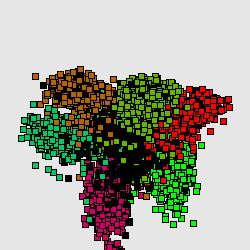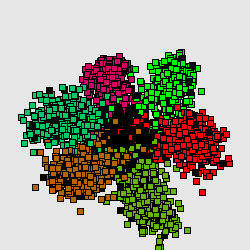
Рис. Б. Проекция ДНК-блуждания на первые 3 главные компоненты для генома бактерии Streptomyces coelicolor. Вращение применяется для визуализации трехмерной конфигурации
Рис. Б. Проекция ДНК-блуждания на первые 3 главные компоненты для генома бактерии Streptomyces coelicolor. Вращение применяется для визуализации трехмерной конфигурации

Метод главных компонент интенсивно используется в биоинформатике для сокращения размерности описания, выделения значимой информации, визуализации данных и др. Один из распространнённых вариантов использования — анализ соответствий (англ. Correspondence Analysis) [1]. На иллюстрациях (Рис. А, Б) генетический текст (см. статью Трансляция (биология)) представлен как множество точек в 64-мерном пространстве частот триплетов. Каждая точка соответствует фрагменту ДНК в скользящем окне длиной 300 нуклеотидов (ДНК-блуждание). Этот фрагмент разбивается на неперекрывающиеся триплеты, начиная с первой позиции. Относительные частоты этих триплетов в фрагменте и составляют 64-мерный вектор. На Рис. А представлена проекция на первые 2 главные компоненты для генома бактерии Streptomyces coelicolor. На Рис. Б представлена проекция на первые 3 главные комроненты. Оттенками красного и коричневого выделены фрагменты кодирующих последовательностей в прямой цепи ДНК, а оттенками зеленого выделены фрагменты кодирующих последовательностей в обратной цепи ДНК. Черным помечены фрагменты, принадлежащие некодирующей части. Анализ методом главных компонент большинства известных бактериальных геномов представлен на специализированном сайте[1].

Хемометрика

Метод главных компонент — один из основных методов в хемометрике (англ. Chemometrics). Позволяет разделить матрицу исходных данных X на две части: «содержательную» и «шум». По наиболее популярному определению [1] «Хемометрика — это химическая дисциплина, применяющая математические, статистические и другие методы, основанные на формальной логике, для построения или отбора оптимальных методов измерения и планов эксперимента, а также для извлечения наиболее важной информации при анализе экспериментальных данных».

Психодиагностика

Психодиагностика является одной из наиболее разработанных областей приложения метода главных компонент [1]. Стратегия использования основывается на гипотезе об автоинформативности экспериментальных данных, которая подразумевает, что диагностическую модель можно создать путем аппроксимации геометрической структуры множества объектов в пространстве исходных признаков. Хорошую линейную диагностическую модель удается построить, когда значительная часть исходных признаков внутренне согласованна. Если эта внутренняя согласованность отражает искомый психологический конструкт, то параметры линейной диагностической модели (веса признаков) дает метод главных компонент.

Общественные науки

Метод главных компонент — один из основных инструментов эконометрики. Он применяется для: (1) наглядного представления данных; (2) обеспечения лаконизма моделей, упрощения счета и интерпретации; (3) сжатия объемов хранимой информации. Метод обеспечивает максимальную информативность и минимальное искажение геометрической структуры исходных данных. В социологии метод небходим для решения первых двух основных задач[1]: (1) анализ данных (описание результатов опросов или других исследований, представленных в виде массивов числовых данных); (2) описание социальных явлений (построение моделей явлений, в том числе и математических моделей). В политологии метод главных компонент был основным инструментом проекта «Политический Атлас Современности»[1] для линейного и нелинейного анализа рейтингов 192 стран мира по пяти специально разработанным интегральным индексам (уровня жизни, международного влияния, угроз, государственности и демократии). Для картографии результатов этого анализа разработана специальная ГИС (Геоинформационная система), объединяющая географическое пространство с пространством признаков.

Сокращение размерности динамических моделей

Проклятие размерности (англ. Curse of dimensionality}}) затрудняет моделирование сложных систем. Сокращение размерности модели — необходимое условие успеха моделирования. Для достижения этой цели создана разветвленная математическая технология. Метод главных компонент также используется в этих задачах (часто под названием истинное или собственное ортогональное разложение — англ. proper orthogonal decomposition (POD)). Например, при описании динамики турбулентности динамические переменные — поле скоростей — принадлежат бесконечномерному пространству (или, если предствлять поле его значениями на достаточно мелкой сетке, — конечномерному пространству большой размерности). Можно набрать большую коллекцию мгновенных значений полей и применить к этому множеству многомерных «векторов данных» метод главных компонент. Эти главные компоненты называются также эмпирические собственные векторы. В некоторых случаях (структурная турбулентность) метод дает впечатляющее сокращение размерности[1] Другие области применения этой техники сокращения динамических моделей чрезвычайно разнообразны — от теоретических основ химической технологии (англ. chemical engineering science) до океанологии и климатологии.

Литература

Классические работы

  • Pearson K., On lines and planes of closest fit to systems of points in space, Philosophical Magazine, (1901) 2, 559—572; а также на сайте PCA.
  • Sylvester J.J., On the reduction of a bilinear quantic of the nth order to the form of a sum of n products by a double orthogonal substitution, Messenger of Mathematics, 19 (1889), 42—46; а также на сайте PCA.
  • Frećhet M. Les élements aléatoires de nature quelconque dans un espace distancié. Ann. Inst. H. Poincaré, 10 (1948), 215—310.

Основные руководства (стандарт де-факто)

  • Айвазян С. А., Бухштабер В. М., Енюков И. С., Мешалкин Л. Д. Прикладная статистика. Классификация и снижение размерности.— М.: Финансы и статистика, 1989.— 607 с.
  • Jolliffe I.T. Principal Component Analysis, Series: Springer Series in Statistics, 2nd ed., Springer, NY, 2002, XXIX, 487 p. 28 illus. ISBN 978-0-387-95442-4

Сборник современных обзоров

Ссылки

Примечания


Источник — «http://machinelearning.ru/wiki/index.php?title=%D0%9C%D0%B5%D1%82%D0%BE%D0%B4_%D0%B3%D0%BB%D0%B0%D0%B2%D0%BD%D1%8B%D1%85_%D0%BA%D0%BE%D0%BC%D0%BF%D0%BE%D0%BD%D0%B5%D0%BD%D1%82»
Личные инструменты