Метод секущих

Материал из MachineLearning.

Версия от 18:44, 23 ноября 2008; Александр Двойнев (Обсуждение | вклад)

(разн.) ← Предыдущая | Текущая версия (разн.) | Следующая → (разн.)

Перейти к: навигация, поиск

Содержание

1 Введение
2 Изложение метода
- 2.1 Геометрическая интерпретация
3 Числовой пример
4 Рекомендации программисту
5 Заключение
6 Ссылки
7 Список литературы

Введение

Пусть задана функция $f(x)$ действительного переменного. Требуется найти корни уравнения

(1)

$f(x)=0.$

Задача нахождения корней уравнения (1) обычно решается в 2 этапа. На первом этапе проводится отделение корней, т.е. выделение отрезков, содержащих только один корень. На втором этапе, используя начальное приближение, строится итерационный процесс, позволяющий уточнить значение отыскиваемого корня.

Изложение метода

Метод секущих получается из метода касательных заменой $f'(x^k)$ разностным приближением:

$f'(x^k) \approx \frac{f(x^k)-f(x^{k-1})}{x^k-x^{k-1}}.$

В результате получим формулу итерационного процесса:

(1)

$x^{k+1}=x^k-\frac{x^k-x^{k-1}}{f(x^k)-f(x^{k-1})}f(x^k), \;k=1,2,\ldots$

Метод секущих является двухшаговым, т.е. новое приближение $x^{k+1}$ определяется двумя предыдущими итерациями $x^k$ и $x^{k-1}.$ В методе (1) необходимо задавать два начальных приближения $x^0$ и $x^1.$

Скорость сходимости метода будет линейной: $|x^{k+1}-x*|=O(k^k-x*).$

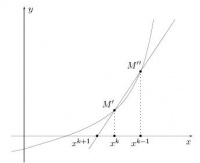
Геометрическая интерпретация

Метод секущих

Заметим, что уравнение для секущей, проходящей через точки $M'(x^{k-1},f(x^{k-1}))$ и $M''(x^k,f(x^k))$ , будет выглядть так:

$\frac{y-f(x^k)}{x-x^k}=\frac{f(x^k)-f(x^{k-1})}{x^k-x^{k-1}}.$

Положив $y=0$ и $x=x^{k+1},$ можно получить формулу (1). Это означает, что $x^{k+1}$ - это абсцисса точки пересечения нашей секущей с осью ОХ. Иначе говоря, на отрезке $[x^{k-1},x^k]$ функция $f(x)$ интерполируется многочленом первой степени и за очередное приближение $x^{k+1}$ принимается корень этого многочлена.