Применение сплайнов для численного интегрирования

Материал из MachineLearning.

Перейти к: навигация, поиск

Содержание

Введение

Ставится задача вычислить интеграл вида

(1)
J=\int_a^bf(t)dt,

где a и b - нижний и верхний пределы интегрирования; f(t) - непрерывная функция на отрезке [a,b].

Пусть на отрезке интегрирования дана сетка, т.е. имеется совокупность узлов \left\{{t_i}\right\}_{i = 0}^{N},\; i\in \left[{a, b}\right]. Тогда интервал [a,b] разобьется на участки \tau_i = t_i-t_{i-1},\; i=1,\dots,N.. Пусть также известны значения функции в узлах этой сетки, т.е. задана таблица f_i = \left\{{f(t_i)}\right\}_{i = 0}^{N}. Представим интеграл (1) в виде суммы интегралов по частичным отрезкам:

(2)
\int_a^bf(t)dt=\sum_{i=1}^N\;\int_{t_{i-1}}^{t_i}f(t)dt.

Сущность большинства методов вычисления определённых интегралов состоит в замене подынтегральной функции f(t) на отрезке [t_{i-1},\;t_i] аппроксимирующей функцией \varphi(t), для которой можно легко записать первообразную в элементарных функциях, т.е.

(3)
\int_{t_{i-1}}^{t_i}f(t)dt=\int_{t_{i-1}}^{t_i}\varphi(t)dt+R_i=S_i+R_i,
(1*)
J=\sum_{i=1}^N \left( \int_{t_{i-1}}^{t_i}\varphi(t)dt+R_i \right)=S+R,

где S_i - приближённое значение интеграла на i-м отрезке, S=\sum_{i=1}^NS_i, а R_i - погрешность вычисления интеграла, R=\sum_{i=1}^NR_i,. Лучше всего изучена замена f(t) алгебраическим многочленом.

Изложение метода

Общий случай

Возьмём в (3) в качестве аппроксимирующей функции кубический сплайн:

(4)
\int_{t_{i-1}}^{t_i}f(t)dt = \int_{t_{i-1}}^{t_i}\varphi_i(t)dt+R_i, где
(φ)
\varphi_i(t) = a_i+b_i(t-t_{i-1})+c_i(t - t_{i-1})^2 + d_i(t - t_{i-1})^3, \; t \in [t_{i-1},\;t_i].

Известно, что коэффициенты a_i, b_i и d_i вычисляются по следующим формулам:

(5a)
a_i=f_{i-1}
(5b)
b_i=\frac{f_i-f_{i-1}}{\tau_i}\;-\;\frac{\tau_i(2c_i+c_{i+1})}{3}
(5d)
d_i=\frac{c_{i+1}-c_i}{3\tau_i}

А коэффициенты c_i являются решением СЛАУ:

(5c)
\tau_{i-1}c_{i-1}+2(\tau_{i-1}+\tau_i)c_i+\tau_i c_{i+1}=3\left(\frac{f_i-f_{i-1}}{\tau_i} \; - \; \frac{f_{i-1}-f_{i-2}}{\tau_{i-1}}\right),\;\; 2 \le i \le N

Нетрудно видеть, что матрица для решения СЛАУ (5c) есть трёхдиагональная матрица с диагональным преобладанием. Поэтому коэффициенты c_i можно вычислить с помощью метода прогонки.

Коэффициенты c_1 и c_{N+1} получаются из условий свободных концов сплайна. Обычно требуют нулевую кривизну на концах сплайна и берут c_1=c_{N+1}=0.

В итоге интеграл (1*) запишется как сумма интегралов от сплайнов:

J=\sum_{i=1}^N\;\int_{t_{i-1}}^{t_i}\varphi_i(t)dt+R=\sum_{i=1}^N\left(a_i\tau_i+{b_i\over2}\tau_i^2+{c_i\over3}\tau_i^3+{d_i\over4}\tau_i^4\right)+R.

Последняя формула упрощается при подстановке в неё выражений (5a), (5b) и (5d) для коэффициентов a_i,\;b_i и d_i:

(6)
J = \sum_{i=1}^N\;\frac{f_i+f_{i-1}}{2}\tau_i\;-\;\sum_{i=1}^N\;\frac{\tau_i^3(c_{i+1}+c_i)}{12}+R.

Случай с равномерной сеткой

Пусть на отрезке [a,b] задана равномерная сетка, т.е. \tau_1=\tau_2=\dots=\tau_N=\tau. Тогда выражение (6) перепишется в виде:

(7)
J\;=\;\frac{\tau}{2}(f_0+f_N)+\tau\sum_{i=1}^{N-1}f_i-\frac{\tau^3}{6}\sum_{i=2}^Nc_i+R.

Просуммируем уравнения (5c) от i=2 до N. Получим:

(8)
6\sum_{i=2}^Nc_i=(c_2+c_N)+\frac{3}{\tau^2}(f_0-f_1+f_N-f_{N-1}).

Подставим (8) в (7) и получим окончательное выражение для J:

(9)
J\;=\;\tau\sum_{i=2}^{N-2}f_i+\frac{\tau}{12}(5f_0+13f_1+13f_{N-1}+5f_N)-\frac{\tau^3}{36}(c_2+c_N)+R

Несмотря на то, что c_2 и c_N все равно придется вычислять методом прогонки, точность и скорость вычисления приближенного значения интеграла будут увеличены за счет сокращения числа слагаемых.

Анализ метода и ошибок

Анализ формулы (6) показывает, что первый член в правой части совпадает с формулой трапеций. Следовательно, второй член характеризует поправку к методу трапеций, которую дает использование сплайнов.

Как следует из формулы (φ), коэффициенты c_i выражаются через вторые производные \varphi_i''(t):

c_i=\frac{1}{2}\varphi_i''(t_{i-1})\approx\frac{1}{2}f_{i-1}''.

Это позволяет оценить второй член правой части формулы (6):

\frac{\tau_i^3}{12}(c_{i-1}+c_i)\approx\frac{\tau_i^3}{12}f_*'',

где f_*'' - вторая производная в некоторой внутренней точке. Полученная оценка показывает, что добавка к формуле трапеций, которую дает использование сплайнов, компенсирует погрешность самой формулы трапеций.

Ошибки округления

Следует помнить, что при реализации метода помимо теоретической априорной погрешности из-за суммы большого числа чисел возникает также погрешность округления.

Числовой пример

рис.1. График функции
рис.1. График функции

Рассмотрим функцию f(t)=sin(t). Вычислим с помощью сплайн-квадратур приближенное значение интеграла

\int_0^ \pi f(t)dt=\int_0^\pi sin(t) dt=2

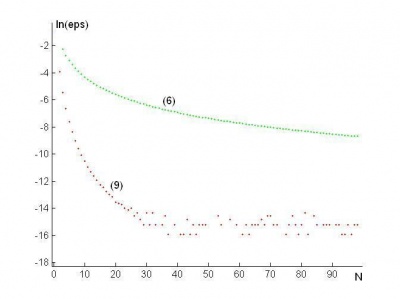
и исследуем поведение погрешности. Результаты работы программы проиллюстрируем в виде графика зависимости логарифма ошибки от числа разбиений:

рис.2. Число разбиений: 100
рис.2. Число разбиений: 100
рис.3. Число разбиений: 1 000 000
рис.3. Число разбиений: 1 000 000

При этом красным цветом показан результат рассчетов по формуле (9), а зеленым - по формуле (6).

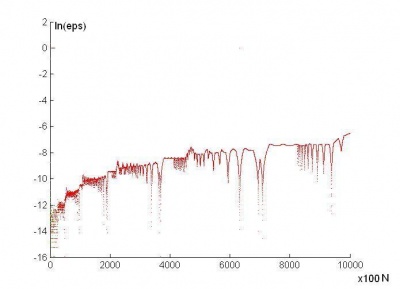
Как видно из рис.2, в данном примере бессмысленно брать число разбиений большее, чем 30. Более того, как видно из рис.3, при большом числе разбиений погрешность начинает расти.

Рекомендации программисту

Пример программы

Ниже приведен пример программы на языке C++, считающей приближенное значение интеграла с помощью сплайн-квадратур: Splineint.zip [0.7Кб]

Некоторые комментарии по работе с программой:

В 6-й строке const int N=1000; N - число отрезков \tau_i.

В 8-й строке const double a=0,b=pi; a и b - пределы интегрирования.

В 18-й строке f[i]=sin(x); f[i] - интегрируемая функция.

Заключение

Итак, мы получили, что погрешность сплайн-квадратуры меньше, чем погрешность метода трапеций. Однако алгоритм интегрирования с помощью сплайнов сложнее алгоритмов методов трапеций и Симпсона за счет необходимости решения СЛАУ для опрееления коэффициентов сплайнов c_i. Также при решении СЛАУ теряется точность. Поэтому рационально использовать сплайн-квадратуры в комплексе, когда сплайны уже используются, в частности, для сглаживания зависимостей, обработки эксперимениальных данных и т.п.

Также одним из основных преимуществ метода является возможность работать с произвольным разбиением орезка.

Ссылки

Список литературы

Источник — «http://machinelearning.ru/wiki/index.php?title=%D0%9F%D1%80%D0%B8%D0%BC%D0%B5%D0%BD%D0%B5%D0%BD%D0%B8%D0%B5_%D1%81%D0%BF%D0%BB%D0%B0%D0%B9%D0%BD%D0%BE%D0%B2_%D0%B4%D0%BB%D1%8F_%D1%87%D0%B8%D1%81%D0%BB%D0%B5%D0%BD%D0%BD%D0%BE%D0%B3%D0%BE_%D0%B8%D0%BD%D1%82%D0%B5%D0%B3%D1%80%D0%B8%D1%80%D0%BE%D0%B2%D0%B0%D0%BD%D0%B8%D1%8F»
Личные инструменты