Проверка гипотезы наличия тренда для количества посетителей сервиса "Яндекс Кубок"

Материал из MachineLearning.

Перейти к: навигация, поиск

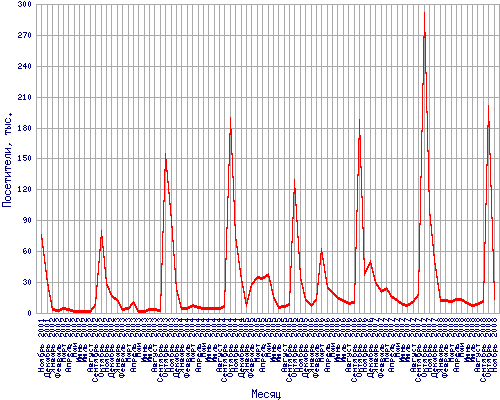
Дана статистика числа посетителей сервиса Яндекс Кубок с марта 2001 года по ноябрь 2008 года. Необходимо проверить гипотезу наличия тренда в выборке с доверительной вероятность \alpha = 0.95.

График числа посещений изображен ниже, сами данные, вследствие открытого доступа к ним и их размера не представлены.

Количество посетителей

Здесь пики приходятся на время проведения кубков Яндекса по поиску в интернете, в остальное время число посетителей мало.

Проверим, есть ли здесь тренд.

Так как мы не можем сказать, что распределение нормально и дисперсия постоянна, то критерий Аббе-Линника здесь не применим.

Сформулируем нулевую гипотезу H_0: существование тренда.

Сначала воспользуемся критерием Фостера-Стюарта.

Статистика критерия для средних имеет вид

d = \sum_{i=2}^n d_i,

где

d_i=u_i-l_i; \quad S_i=u_i+l_i;
  • если x_i>x_{i-1},\ldots,x_1, то u_i=1, в противном случае u_i=0
  • если x_i<x_{i-1},\ldots,x_1, то l_i=1, в противном случае l_i=0

Получилось d=-1

При отсутствии тренда величина

t=\frac d f, где
f=\sqrt{2\ln{n}-0.8456}

имеет распределение Стьюдента с \nu=n степенями свободы.

После вычислений получаем: |t|=0.35.

\gamma-квантиль распределения Стьюдента с \nu=n степенями свободы t_{\frac{1+\alpha}2}=t_{0.975}=0.03

|t|=0.35>t_{\frac{1+\alpha}2}=t_{0.975}=0.03, поэтому нулевая гипотеза H_0 существования тренда принимается.

Теперь воспользуемся критерием Кокса-Стюарта.

Сначала посчитаем статистику S_1:

S_1 = \sum_{i=1}^{[\frac{n}{2}]}(n-2i+1)h_{i,n-i+1}, где
h_{i,j} = \begin{cases} 0, & x_i>x_j; \\ 1, & x_i \leq x_j. \end{cases} \quad (i<j)

Получилось: S_1 = 308

Теперь посчитаем нормализованную статистику S_1^*

S_1^* = \frac{S_1 - M(S_1)}{\sqrt{D(S_1)}, где
M(S_1) = \frac{n^2}8 и
D(S_1) = \frac{n(n^2-1)}{24} .

Получилось S_1^* = -3.72

При |S_1^*| < u_{\frac{1+\alpha}2} гипотеза H_0 существования тренда среднего отклоняется (u_\gamma - \gamma-квантиль нормального распределения).

|S_1^*|=3.72 > u_{0.975} = 1.96, поэтому нулевая гипотеза H_0 существования тренда принимается.

В заключение, стоит отметить, что критерий Кокса-Стюарта намного более быстрый чем критерий Фостера-Стюарта. Если в критерие Кокса-Стюарта сложность вычислений зависит линейно от объема данных, то в критерие Фостера-Стюарта зависимость квадратичная. Поэтому при больших объемах данных критерий Кокса-Стюарта оказывается более предпочтительным.

В данной задаче оба критерия дали один и тот же результат.

Литература

  1. Кобзарь А. И. Прикладная математическая статистика. — М.: Физматлит, 2006. — 816 с.

См. также

Источник — «http://machinelearning.ru/wiki/index.php?title=%D0%9F%D1%80%D0%BE%D0%B2%D0%B5%D1%80%D0%BA%D0%B0_%D0%B3%D0%B8%D0%BF%D0%BE%D1%82%D0%B5%D0%B7%D1%8B_%D0%BD%D0%B0%D0%BB%D0%B8%D1%87%D0%B8%D1%8F_%D1%82%D1%80%D0%B5%D0%BD%D0%B4%D0%B0_%D0%B4%D0%BB%D1%8F_%D0%BA%D0%BE%D0%BB%D0%B8%D1%87%D0%B5%D1%81%D1%82%D0%B2%D0%B0_%D0%BF%D0%BE%D1%81%D0%B5%D1%82%D0%B8%D1%82%D0%B5%D0%BB%D0%B5%D0%B9_%D1%81%D0%B5%D1%80%D0%B2%D0%B8%D1%81%D0%B0_%22%D0%AF%D0%BD%D0%B4%D0%B5%D0%BA%D1%81_%D0%9A%D1%83%D0%B1%D0%BE%D0%BA%22»
Личные инструменты