Распространение ошибок

Материал из MachineLearning.

Содержание

1 Введение
2 Распространение ошибок
- 2.1 Абсолютная ошибка
- 2.2 Относительная ошибка
3 Графы вычислительных процессов
- 3.1 Примеры
4 Памятка программисту
5 Список литературы
6 См. также

Введение

Одним из наиболее важных вопросов в численном анализе является вопрос о том, как ошибка, возникшая в определенном месте в ходе вычислений, распространяется дальше, то есть становится ли ее влияние больше или меньше по мере того, как производятся последующие операции. Крайним случаем является вычитание двух почти равных чисел: даже при очень маленьких ошибках обоих этих чисел относительная ошибка разности может оказаться очень большой. Такая относительная ошибка будет распространяться дальше при выполнении всех последующих арифметических операций.

Одним из источников вычислительных погрешностей (ошибок) является приближенное представление вещественных чисел в ЭВМ, обусловленное конечностью разрядной сетки. Хотя исходные данные представляются в ЭВМ с большой точностью накопление погрешностей округления в процессе счета может привести к значительной результирующей погрешности, а некоторые алгоритмы могут оказаться и вовсе непригодными для реального счета на ЭВМ. Подробнее о представлении вещественных чисел в ЭВМ можно узнать здесь.

Распространение ошибок

В качестве первого шага при рассмотрении такого вопроса, как распространение ошибок, необходимо найти выражения для абсолютной и относительной ошибок результата каждого из четырех арифметических действий как функции величин, участвющих в операции, и их ошибок.

Абсолютная ошибка

Сложение

Имеются два приближения $\bar{x}$ и $\bar{y}$ к двум величинам $x$ и $y$ , а также соответствующие абсолютные ошибки $e_x$ и $e_y$ . Тогда в результате сложения имеем

$x+y=\bar{x}+e_x+\bar{y}+e_y=(\bar{x}+\bar{y})+(e_x+e_y)$ .

Ошибка суммы, которую мы обозначим через $e_{x+y}$ , будет равна

$e_{x+y}=e_x+e_y$ .

Вычитание

Тем же путем получаем

$e_{x-y}=e_x-e_y$ .

Умножение

При умножении мы имеем

$x\cdot y=(\bar{x}+e_x)\cdot (\bar{y}+e_y)=\bar{x}\bar{y}+\bar{x}e_y+\bar{y}e_x+e_xe_y$ .

Поскольку ошибки обычно гораздо меньше самих величин, пренебрегаем произведением ошибок:

$x\cdot y\approx \bar{x}\bar{y}+\bar{x}e_y+\bar{y}e_x$ .

Ошибка произведения будет равна

$e_{xy}\approx \bar{x}e_y+\bar{y}e_x$ .

Деление

Имеем

$\frac{x}{y}=\frac{\bar{x}+e_x}{\bar{y}+e_y}$ .

Преобразовываем это выражение к виду

$\frac{x}{y}=\frac{\bar{x}+e_x}{\bar{y}}\cdot \left(\frac{1}{1+\frac{e_y}{\bar{y}}}\right)$ .

Множитель, стоящий в скобках, при $\left| \frac{e_y}{\bar{y}}\right|<<1$ можно разложить в ряд

$\frac{x}{y}=\frac{\bar{x}+e_x}{\bar{y}}\cdot \left(1-\frac{e_y}{\bar{y}}+\left(\frac{e_y}{\bar{y}}\right)^2-\ldots \right)$ .

Перемножая и пренебрегая всеми членами, которые содержат произведения ошибок или степени ошибок выше первой, имеем

$\frac{x}{y}\approx \frac{\bar{x}}{\bar{y}}+\frac{e_x}{\bar{y}}-\frac{\bar{x}}{\bar{y}^2}e_y$ .

Следовательно,

$e_{x/y}\approx \frac{1}{\bar{y}}e_x-\frac{\bar{x}}{\bar{y}^2}e_y$ .

Необходимо четко понимать, что знак ошибки бывает известен только в очень редких случаях. Не факт, например, что ошибка увеличивается при сложении и уменьшается при вычитании потому, что в формуле для сложения стоит плюс, а для вычитания — минус. Если, например, ошибки двух чисел имеют противоположные знаки, то дело будет обстоять как раз наоборот, то есть ошибка уменьшится при сложении и увеличится при вычитании этих чисел.

Относительная ошибка

После того, как мы вывели формулы для распространения абсолютных ошибок при четырех арифметических действиях, довольно просто вывести соответствующие формулы для относительных ошибок. Для сложения и вычитания формулы были преобразованы с тем, чтобы в них входила в явном виде относительная ошибка каждого исходного числа.

Сложение

$\frac{e_{x+y}}{\bar{x}+\bar{y}}=\frac{\bar{x}}{\bar{x}+\bar{y}}(\frac{e_x}{\bar{x}})+\frac{\bar{y}}{\bar{x}+\bar{y}}(\frac{e_y}{\bar{y}})$ .

Вычитание

$\frac{e_{x-y}}{\bar{x}-\bar{y}}=\frac{\bar{x}}{\bar{x}-\bar{y}}(\frac{e_x}{\bar{x}})-\frac{\bar{y}}{\bar{x}-\bar{y}}(\frac{e_y}{\bar{y}})$ .

Умножение

$\frac{e_{x\cdot y}}{\bar{x}\cdot \bar{y}}=\frac{e_x}{\bar{x}}+\frac{e_y}{\bar{y}}$ .

Деление

$\frac{e_{x/y}}{\bar{x}/\bar{y}}=\frac{e_x}{\bar{x}}-\frac{e_y}{\bar{y}}$ .

Мы начинаем арифметическую операцию, имея в своем распоряжении два приближенных значения $\bar{x}$ и $\bar{y}$ с соответствующими ошибками $e_x$ и $e_y$ . Ошибки эти могут быть любого происхождения. Величины $\bar{x}$ и $\bar{y}$ могут быть экспериментальными результатами, содержащими ошибки; они могут быть результатами предварительного вычисления согласно какому-либо бесконечному процессу и поэтому могут содержать ошибки ограничения; они могут быть результатами предшествующих арифметических операций и могут содержать ошибки округления. Естественно, они могут также содержать в различных комбинациях и все три вида ошибок.

Вышеприведенные формулы дают выражение ошибки результата каждого из четырех арифметических действий как функции от $\bar{x},\bar{y},e_x, e_y$ ; ошибка округления в данном арифметическом действии при этом не учитывается. Если же в дальнейшем необходимо будет подсчитать, как распространяется в последующих арифметических операциях ошибка этого результата, то необходимо к вычисленной по одной из четырех формул ошибке результата прибавить отдельно ошибку округления.

Графы вычислительных процессов

Теперь рассмотрим удобный способ подсчета распространения ошибки в каком-либо арифметическом вычислении. С этой целью мы будем изображать последовательность операций в вычислении с помощью графа и будем писать около стрелок графа коэффициенты, которые позволят нам сравнительно легко определить общую ошибку окончательного результата. Метод этот удобен еще и тем, что позволяет легко определить вклад любой ошибки, возникшей в процессе вычислений, в общую ошибку.

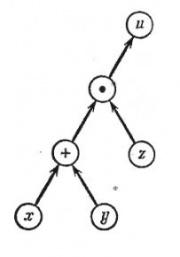
Рис.1. Граф вычислительного процесса $u=(x+y)\cdot z$

На рис.1 изображен граф вычислительного процесса $u=(x+y)\cdot z$ . Граф следует читать снизу вверх, следуя стрелкам. Сначала выполняются операции, расположенные на каком-либо горизонтальном уровне, после этого — операции, расположенные на более высоком уровне, и т. д. Из рис.1, например, ясно, что x и y сначала складываются, а потом умножаются на z. Граф, изображенный на рис.1, является только изображением самого вычислительного процесса. Для подсчета общей ошибки результата необходимо дополнить этот граф коэффициентами, которые пишутся около стрелок согласно следующим правилам.

Сложение

Пусть две стрелки, которые входят в кружок сложения, выходят из двух кружков с величинами $a_1$ и $a_2$ . Эти величины могут быть как исходными, так и результатами предыдущих вычислений. Тогда стрелка, ведущая от $a_1$ к знаку + в кружке, получает коэффициент $a_1/(a_1+a_2)$ , стрелка же, ведущая от $a_2$ к знаку + в кружке, получает коэффициент $a_2/(a_1+a_2)$ .

Вычитание

Если выполняется операция $a_1-a_2$ , то соответствующие стрелки получают коэффициенты $a_1/(a_1-a_2)$ и $a_2/(a_1-a_2)$ .

Умножение

Обе стрелки, входящие в кружок умножения, получают коэффициент +1.

Деление

Если выполняется деление $a_1/a_2$ , то стрелка от $a_1$ к косой черте в кружке получает коэффициент +1, а стрелка от $a_2$ к косой черте в кружке получает коэффициент −1.

Смысл всех этих коэффициентов следующий: относительная ошибка результата любой операции (кружка) входит в результат следующей операции, умножаясь на коэффициенты у стрелки, соединяющей эти две операции.

Примеры

Рис.2. Граф вычислительного процесса для сложения , причем

Рис.2. Граф вычислительного процесса для сложения $y=x_1+x_2+x_3+x_4$ , причем $0<x_1<x_2<x_3<x_4$

Применим теперь методику графов к примерам и проиллюстрируем, что означает распространение ошибки в практических вычислениях.

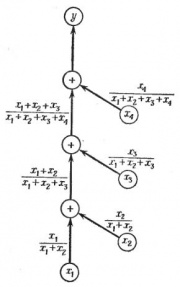
Пример 1

Рассмотрим задачу сложения четырех положительных чисел:

$y=x_1+x_2+x_3+x_4$ ,

где

$0<x_1<x_2<x_3<x_4$ .

Граф этого процесса изображен на рис.2. Предположим, что все исходные величины заданы точно и не имеют ошибок, и пусть $r_1$ , $r_2$ и $r_3$ являются относительными ошибками округления после каждой следующей операции сложения. Последовательное применение правила для подсчета полной ошибки окончательного результата приводит к формуле

$\frac{e_y}{y}=r_1\frac{x_1+x_2}{x_1+x_2+x_3}\cdot \frac{x_1+x_2+x_3}{x_1+x_2+x_3+x_4}+r_2\frac{x_1+x_2+x_3}{x_1+x_2+x_3+x_4}+r_3$ .

Сокращая сумму $x_1+x_2+x_3$ в первом члене и умножая все выражение на $y=x_1+x_2+x_3+x_4$ , получаем

$e_y=r_1(x_1+x_2)+r_2(x_1+x_2+x_3)+r_3(x_1+x_2+x_3+x_4)$ .

Учитывая, что ошибка округления равна $5\cdot 10^{-t}$ (в данном случае предполагается, что действительное число в ЭВМ представляется в виде десятичной дроби с t значищими цифрами), окончательно имеем

$|e_y|\leq (3x_1+3x_2+2x_3+x_4)\cdot 5\cdot 10^{-t}$ .

Из этой формулы ясно, что максимально возможная ошибка (абсолютная или относительная), обусловленная округлением, становится меньше, если сначала складывать меньшие числа. Результат довольно удивительный, так как вся классическая математика основана на предположении, что при перемене мест слагаемых или их группировке сумма не изменяется. Разница заключается в том, что ЭВМ не может производить вычисления с бесконечно большой точностью, а именно такие вычисления рассматриваются в классической математике.

Пример 2

Вычитание двух почти равных чисел. Предположим, что необходимо вычислить $z=x-y$ . Тогда из формулы распространения ошибки при вычитании имеем

$\frac{e_z}{z}=\frac{x}{x-y}\left(\frac{e_x}{x}\right)-\frac{y}{x-y}\left(\frac{e_y}{y}\right)$ .

Предположим, кроме того, что x и y являются соответствующим образом округленными положительными числами, так что

$\left|\frac{e_x}{x}\right|\leq 5\cdot 10^{-t}$ и $\left|\frac{e_y}{y}\right|\leq 5\cdot 10^{-t}$ .

Если разность x-y мала, то относительная ошибка z может стать большой, даже если абсолютная ошибка мала. Так как в дальнейших вычислениях эта большая относительная ошибка будет распространяться, то она может поставить под сомнение точность окончательного результата вычислений.

Рассмотрим простой пример:

$x=0.5628\cdot 10^4$

$y=0.5631\cdot 10^4$

Тогда

$z=-0.0003\cdot 10^4$

Зная x и y, мы можем написать

$\left|\frac{e_x}{x}\right|\leq \frac{0.5}{0.5628}\cdot 10^{-4}<0.01%$

$\left|\frac{e_y}{y}\right|\leq \frac{0.5}{0.5631}\cdot 10^{-4}<0.01%$

Как видим, относительные ошибки x и y малы. Однако

$\left|\frac{e_z}{z}\right|\leq \frac{1}{0.0003}\cdot 10^{-4}\approx 33%$

Эта относительная ошибка очень велика, и, что важнее всего, она будет распространяться в ходе последующих вычислений.

Памятка программисту

Выводы, полученные выше, можно свести в краткий перечень рекомендаций для практической организации вычислений.

Если необходимо произвести сложение-вычитание длинной последовательности чисел, работайте сначала с наименьшими числами.
Если возможно, избегайте вычитания двух почти равных чисел. Формулы, содержащие такое вычитание, часто можно преобразовать так, чтобы избежать подобной операции.
Выражение вида $a(b-c)$ можно написать в виде $ab-ac$ , а выражение вида $(b-c)/a$ можно написать в виде $b/a-c/a$ . Если числа в разности почти равны друг другу, производите вычитание до умножения или деления. При этом задача не будет осложнена дополнительными ошибками округления.
В любом случае сводите к минимуму число необходимых арифметических операций.

Список литературы

Д.Мак-Кракен, У.Дорн. Численные методы и программирование на Фортране. Москва «Мир», 1977
А. А. Самарский, А. В. Гулин. Численные методы. Москва «Наука», 1989.

См. также

Практикум ММП ВМК, 4й курс, осень 2008

Источник — «http://machinelearning.ru/wiki/index.php?title=%D0%A0%D0%B0%D1%81%D0%BF%D1%80%D0%BE%D1%81%D1%82%D1%80%D0%B0%D0%BD%D0%B5%D0%BD%D0%B8%D0%B5_%D0%BE%D1%88%D0%B8%D0%B1%D0%BE%D0%BA»

Категория: Численные методы

Распространение ошибок

Материал из MachineLearning.

Содержание

Введение

Распространение ошибок

Абсолютная ошибка

Относительная ошибка

Графы вычислительных процессов

Примеры

Памятка программисту

Список литературы

См. также

Просмотры

Личные инструменты

Навигация

Поиск

Инструменты