Участник:Александр Двойнев/песочница
Материал из MachineLearning.
(→Заключение) |
|||
| Строка 1: | Строка 1: | ||
== Введение == | == Введение == | ||
| - | |||
| - | |||
| - | |||
| - | |||
| - | Пусть | + | Пусть задана функция <tex>f(x)</tex> действительного переменного. Требуется найти корни уравнения |
| - | + | {{eqno|1}} | |
| - | + | ::<tex>f(x)=0.</tex> | |
| - | <tex> | + | |
| - | + | ||
| - | + | ||
| - | ::<tex> | + | |
| - | + | Задача нахождения корней уравнения {{eqref|1}} обычно решается в 2 этапа. На первом этапе проводится отделение корней, т.е. выделение отрезков, содержащих только один корень. На втором этапе, используя начальное приближение, строится итерационный процесс, позволяющий уточнить значение отыскиваемого корня. | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
== Изложение метода == | == Изложение метода == | ||
| - | |||
| - | |||
| - | |||
| - | |||
| - | + | ===Метод касательных (Ньютона-Рафсона)=== | |
| - | + | ||
| - | + | Пусть на отрезке <tex>[a,b]</tex> существует единственный корень уравнения {{eqref|1}}: <tex>x*</tex> | |
| - | {{eqno| | + | {{eqno|2}} |
| - | ::<tex> | + | ::<tex>f(x*)=0</tex>, |
| + | а <tex>f'(x)</tex> существует, непрерывна и отлична от нуля на <tex>[a,b]</tex>. Перепишем {{eqref|2}} следующим образом: | ||
| + | ::<tex>f(x^k+(x*-x^k))=0</tex> | ||
| + | и применим к этому выражению [[формула Лагранжа|формулу Лагранжа]]: | ||
| + | ::<tex>f(x^k)+f'(\bar{x})(x*-x^k)=0, \;\bar{x} \in [a,b].</tex> | ||
| + | Заменим <tex> \bar x</tex> на <tex>x^k</tex>, а <tex>x*</tex> - на <tex>x^{k+1}</tex> и получим формулу итерационного процесса: | ||
| + | ::<tex>f(x^k)+f'(x^k)(x^{k+1}-x^k)=0.</tex> | ||
| + | Выразим отсюда <tex>x^{k+1}</tex>: | ||
| + | {{eqno|3}} | ||
| + | ::<tex>x^{k+1}=x^k-\frac{f(x^k)}{f'(x^k)}.</tex> | ||
| - | + | Метод касательных имеет (когда сходится) квадратичную скорость сходимости: <tex>|x^{k+1}-x*|=O((x^k-x*)^2).</tex> | |
| - | + | ||
| - | + | ===Модифицированный метод касательных=== | |
| - | + | ||
| - | + | Если мы хотим избежать вычисления производной на каждом шаге, то можно взять <tex> f'(x^0)</tex> вместо <tex>f'(x),</tex> где <tex>x^0</tex> - начальное приближение: | |
| - | + | ::<tex>x^{k+1}=x^k-\frac{f(x^k)}{f'(x^0)}.</tex> | |
| - | ::<tex> | + | В отличие от обычного метода касательных, в модифицированном методе предоставляется меньше требований к выбору начального приближения, а так же гарантировано отсутствие деления на ноль, если <tex>f'(x^0) \ne 0.</tex> |
| - | + | ||
| - | + | Однако модифицированный метод имеет один существенный недостаток: линейную скорость сходимости: <tex>|x^{k+1}-x*|=O(x^k-x*).</tex> | |
| - | + | === Геометрическая интерпретация=== | |
| - | : | + | [[Изображение:kasat.jpg|thumb|200px|Метод касательных]] |
| + | Метод Ньютона-Рафсона называют также методом касательных, т.к. новое приближение <tex>x^{k+1}</tex> является абсциссой точки пересечения касательной, проведенной в точке <tex>(x^k,f(x^k))</tex> к графику функции <tex>f(x)</tex>, с осью ОХ. | ||
| - | + | == Сходимость метода == | |
| - | + | Заметим, что метод касательных является частным случаем [[Метод простых итераций|метода простых итераций]] | |
| - | ::<tex> | + | ::<tex>x^{k+1}=g(x^k),\; k=0,1,\ldots,</tex> |
| + | для которого | ||
| + | {{eqno|4}} | ||
| + | ::<tex>g(x)=x-\frac{f(x)}{f'(x)}.</tex> | ||
| - | + | [[Метод простых итераций]] сходится тогда и только тогда, когда | |
| + | ::<tex>|g'(x)|\le q < 1,</tex> | ||
| - | + | Подставим в последнее условие выражение для g(x) {{eqref|4}} и получим условие сходимости метода касательных: | |
| + | ::<tex>\left|\frac{f(x)f''(x)}{(f'(x))^2}\right| \le q < 1.</tex> | ||
| - | + | Сформулируем теорему о квадратичной скорости сходимости метода касательных: | |
| - | : | + | |
| - | + | '''Теорема.''' Пусть <tex>x*</tex> - простой вещественный корень уравнения <tex>f(x) = 0</tex>, а функция <tex>f(x)</tex> - дважды дифференцируема в некоторой окрестности <tex>U_r(x*)</tex>, причем первая произодная нигде не обращается в нуль. | |
| - | + | Тогда, следуя обозначениям | |
| - | ::<tex> | + | ::<tex>0 < m_1 = \;\inf_{x\in U_r(x*)}|f'(x)|,\;\; M_2 = \;\sup_{x\in U_r(x*)}|f''(x)|</tex>, |
| - | + | при выборе начального приближения <tex>x^0</tex> из той же окрестности <tex>U_r(x^*)</tex> такого, что | |
| - | + | ::<tex>\frac{M_2|x^0 - x*|}{2m_1} = q < 1</tex>, | |
| - | + | итерационная последовательность | |
| - | + | ::<tex>x^{k+1} = x^k - \frac{f(x^k)}{f'(x^k)},\; k = 0,1,\ldots</tex> | |
| - | + | будет сходиться к <tex>x*</tex>, причем для погрешности на k-м шаге буддет справедлива оценка: | |
| - | + | ::<tex>|x^k - x*| \le q^{2^k - 1}|x^0 - x*|.</tex> | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | ::<tex> | + | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | ::<tex> | + | |
| - | + | ||
| - | + | ||
== Числовой пример == | == Числовой пример == | ||
| - | + | Рассмотрим функцию <tex>f(x)= | |
| - | Рассмотрим функцию <tex>f( | + | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
== Рекомендации программисту == | == Рекомендации программисту == | ||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
== Заключение == | == Заключение == | ||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
== Ссылки == | == Ссылки == | ||
* [[Практикум ММП ВМК, 4й курс, осень 2008|Практикум ММП ВМК, 4й курс, осень 2008]] | * [[Практикум ММП ВМК, 4й курс, осень 2008|Практикум ММП ВМК, 4й курс, осень 2008]] | ||
| - | * [[ | + | * [[Метод секущих]] |
| - | + | ||
== Список литературы == | == Список литературы == | ||
| - | * http:// | + | *[http://mmphome.1gb.ru/index.php?pid=show&id=79 Н.В.Соснин. Численные методы. Конспект лекций (сост. Д.В.Ховратович, Е.А.Попов)] |
| - | + | *Самаский А.А., Гулин А.В. Численные Методы. Учеб. пособие для вузов. - М.:Наука, 1989. | |
| - | + | ||
| - | * А. | + | <!--{{Stub|}}--> |
Версия 11:57, 4 декабря 2008
Содержание |
Введение
Пусть задана функция действительного переменного. Требуется найти корни уравнения
Задача нахождения корней уравнения (1) обычно решается в 2 этапа. На первом этапе проводится отделение корней, т.е. выделение отрезков, содержащих только один корень. На втором этапе, используя начальное приближение, строится итерационный процесс, позволяющий уточнить значение отыскиваемого корня.
Изложение метода
Метод касательных (Ньютона-Рафсона)
Пусть на отрезке существует единственный корень уравнения (1):
,
а существует, непрерывна и отлична от нуля на
. Перепишем (2) следующим образом:
и применим к этому выражению формулу Лагранжа:
Заменим на
, а
- на
и получим формулу итерационного процесса:
Выразим отсюда :
Метод касательных имеет (когда сходится) квадратичную скорость сходимости:
Модифицированный метод касательных
Если мы хотим избежать вычисления производной на каждом шаге, то можно взять вместо
где
- начальное приближение:
В отличие от обычного метода касательных, в модифицированном методе предоставляется меньше требований к выбору начального приближения, а так же гарантировано отсутствие деления на ноль, если
Однако модифицированный метод имеет один существенный недостаток: линейную скорость сходимости:
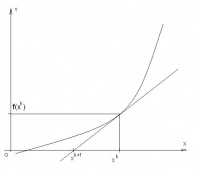
Геометрическая интерпретация
Метод Ньютона-Рафсона называют также методом касательных, т.к. новое приближение является абсциссой точки пересечения касательной, проведенной в точке
к графику функции
, с осью ОХ.
Сходимость метода
Заметим, что метод касательных является частным случаем метода простых итераций
для которого
Метод простых итераций сходится тогда и только тогда, когда
Подставим в последнее условие выражение для g(x) (4) и получим условие сходимости метода касательных:
Сформулируем теорему о квадратичной скорости сходимости метода касательных:
Теорема. Пусть - простой вещественный корень уравнения
, а функция
- дважды дифференцируема в некоторой окрестности
, причем первая произодная нигде не обращается в нуль.
Тогда, следуя обозначениям
,
при выборе начального приближения из той же окрестности
такого, что
,
итерационная последовательность
будет сходиться к , причем для погрешности на k-м шаге буддет справедлива оценка:
Числовой пример
Рассмотрим функцию